Câu 7. Một cuộc đua thuyền xuất phát từ điểm A như hình vẽ dưới và di chuyển theo hướng tây nam một góc 52° tới điểm B, sau đó di chuyển theo hướng đông nam một góc 40° tới điểm C, cuối cùng quay về điểm A. Điểm C cách điểm A một khoảng 8km. Tính gần đúng tổng khoảng cách của đường đua. и
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo đinh lý Pytago: \(\left(30\sqrt{2}\cdot cos45^o\right)-20=10m\)
Về phía Nam.
Chọn C.

Chọn A.
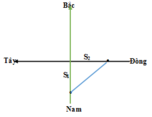
Gọi vận tốc của ca nô là v km/h.
Đổi 18 phút = 0,3 giờ, 24 phút = 0,4 giờ
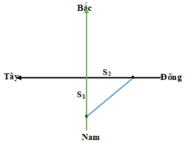
Quãng đường mà ca nô đi được theo hướng Nam - Bắc là: S1 = 0,3.v
Quãng đường mà ca nô đi được theo hướng Đông - Tây là: S2 = 0,4.v
Từ hình vẽ, ta có: = S2 = 252
→ 0,09v2 + 0,16v2 = 625 → v = 50 km/h

Chọn A.
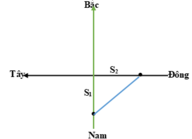
Gọi vận tốc của ca nô là v km/h.
Đổi 18 phút = 0,3 giờ, 24 phút = 0,4 giờ
Quãng đường mà ca nô đi được theo hướng Nam - Bắc là: S 1 = 0,3.v
Quãng đường mà ca nô đi được theo hướng Đông - Tây là: S 2 = 0,4.v
Từ hình vẽ, ta có: S 1 2 + S 2 2 = S 2 = 25 2
→ 0,09 v 2 + 0,16 v 2 = 625
→ v = 50 km/h

Chọn đáp án A
Gọi vận tốc của ca nô là v km/h.
Đổi 18 phút = 0,3 giờ, 24 phút = 0,4 giờ
Quãng đường mà ca nô đi được theo hướng Nam - Bắc là s 1 = 0 , 3. v
Quãng đường mà ca nô đi được theo hướng Đông - Tây là s 2 = 0 , 4. v
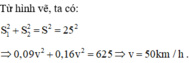

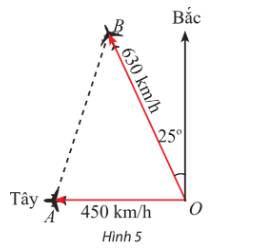
Ta có: \(\widehat {BOA} = {90^o} - {25^o} = {65^o}.\)
Sau 90 phút = 1,5 giờ:
Máy bay thứ nhất đi được quãng đường (OA) là: \(450.1,5 = 675\;(km)\)
Máy bay thứ hai đi được quãng đường (OB) là: \(630.1,5 = 945\;(km)\)
Áp dụng định lí cosin trong tam giác OAB, ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2OA.OB\cos O\\ \Leftrightarrow A{B^2} = {675^2} + {945^2} - 2.675.945\cos {65^o}\\ \Rightarrow AB \approx 900\end{array}\)
Vậy sau 90 phút, hai máy bay cách nhau khoảng 900 km.

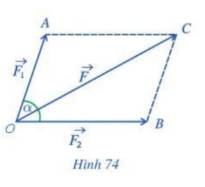
Ta có: \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB}= \overrightarrow {AC} \)
Khi đó: Hợp lực \(\overrightarrow F \) là \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \).
Áp dụng định lí cosin cho tam giác OAC, ta có:
\(\begin{array}{*{20}{l}}
{\;\;\;{\mkern 1mu} {\kern 1pt} \;O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos A}\\
\begin{array}{l}
\Leftrightarrow O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos ({180^o} - \alpha )\\
\Leftrightarrow O{C^2} = O{A^2} + A{C^2} + 2.OA.AC.\cos \alpha
\end{array}\\
{ \Leftrightarrow \left| {\vec F} \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2} + 2.\left| {\overrightarrow {{F_1}} } \right|.\left| {\overrightarrow {{F_2}} } \right|.\cos \alpha } }
\end{array}\)

Vẽ hình:
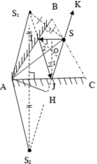
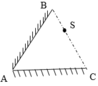
a) S1 là ảnh của S qua gương AB => S1 đối xứng với S qua AB
S2 là ảnh của S1 qua gương AC => S2 đối xứng với S 1 qua AC
Ta nối S2 với S cắt AC tại J, nối J với S1 cắt AB tại I
=> SI, IJ, JS là ba đoạn của tia sáng cần dựng.
b) Dựng hai phỏp tuyến tại I và J cắt nhau tai O
Góc tạo bởi tia phản xạ JK và tia tới SI là ∠ ISK
Theo tính chất góc ngoài tam giác ta có
I S K ^ = I ^ + J ^ = 2 I ^ 2 + 2 J ^ 2 = 2 ( 180 0 − I O ^ J ) = 2. B A ^ C = 120 0
c) Tổng độ dài ba đoạn:
SI + IJ + JS = S1I + IJ + JS = S1J + JS = S2J + JS = S2S
(Đối xứng trục)
Vậy SI + IJ + JS = S2S
Ta có:
∠ S1AS = 2 ∠ S1AB (1)
∠ S1AS2 = 2 ∠ S1AC (2)
Lấy (2) – (1):
∠ S1AS2 - ∠ S1AS = 2( ∠ S1AC - ∠ S1AB)
ð ∠ SAS2 = 2 ∠ BAC
ð ∠ SAS2 = 1200
Xét tam giác cân SAS2 tại A, có ∠ A = 1200
ð ∠ ASH = ∠ AS2H = 300 với đường cao AH, ta có: SS2 = 2SH
Xét tam giác vuông SAH taị H có ∠ ASH = 300 ta có: AH = AS/2
Trong tam giác vuông SAH tại H.
Theo định lí pitago ta tính được SH= S A . 3 2
nên SS2 = 2SH = 2. S A . 3 2 = SA 3
=> SS2 nhỏ nhất ó SA nhỏ nhất ó AS là đường cao của tam giác đều ABC
ó S là trung điểm của BC.
mấy dòng cúi đọc chả hiểu j nhưng mình vẫn chép
thank you so much
I LOVE YOU chụt chụt...

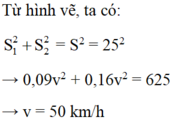

Bạn ơi, hình vẽ đâu vậy bạn?