cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O. Gọi E,F lần lượt là trung điểm SA, SB
a) chứng minh OE // (SCD)
b) chứng minh OF // (SCD)
c) chứng minh (OEF) // (SCD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 11 2023
a: Xét ΔASC có
O,E lần lượt là trung điểm của AC,AS
=>OE là đường trung bình của ΔASC
=>OE//SC
OE//SC
\(SC\subset\left(SCD\right)\)
OE không nằm trong mp(SCD)
Do đó: OE//(SCD)
b: Xét ΔBSD có
O,F lần lượt là trung điểm của BD,BS
=>OF là đường trung bình của ΔBSD
=>OF//SD
OF//SD
SD\(\subset\left(SCD\right)\)
OF không nằm trong (SCD)
Do đó: OF//(SCD)
c: OF//(SCD)
OE//(SCD)
OF,OE cùng thuộc mp(OEF)
Do đó: (OEF)//(SCD)
8 tháng 11 2023
a: Xét ΔASC có
O,M lần lượt là trung điểm của AC,AS
=>OM là đường trung bình
=>OM//SC
Xét ΔSAB có
M,N lần lượt là trung điểm của SA,SB
=>MN là đường trungbình của ΔSAB
=>MN//AB
=>MN//CD
MN//CD
\(CD\subset\left(SCD\right)\)
\(MN\) không thuộc mp(SCD)
Do đó: MN//(SCD)
OM//SC
\(SC\subset\left(SCD\right)\)
OM không thuộc mp(SCD)
Do đó: OM//(SCD)
OM//(SCD)
MN//(SCD)
\(OM,MN\subset\left(OMN\right)\)
Do đó: (OMN)//(SCD)
b: MN//AB
\(AB\subset\left(ABCD\right)\)
MN không thuộc mp(ABCD)
Do đó: MN//(ABCD)
31 tháng 10 2023
a:
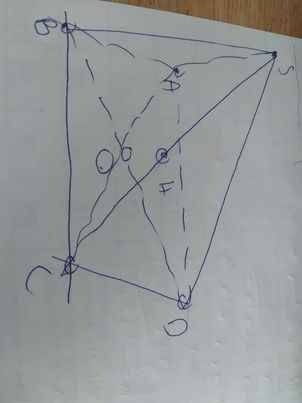
b: ABCD là hình chữ nhật
=>AB//CD và BC//AD
BC//AD
\(AD\subset\left(SAD\right)\)
BC không nằm trong mp(SAD)
Do đó: BC//(SAD)
c: AB//CD
\(CD\subset\left(SCD\right)\)
AB không nằm trong mp(SCD)
Do đó: AB//(SCD)
d: Xét ΔSAC có
O,H lần lượt là trung điểm của CA,CS
=>OH là đường trung bình của ΔSAC
=>OH//SA
OH//SA
\(SA\subset\left(SAB\right)\)
OH không nằm trong mp(SAB)
Do đó: OH//(SAB)
27 tháng 10 2023
a: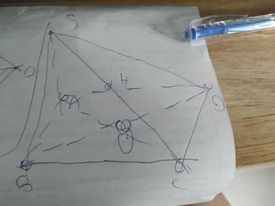 
b: BC//AD(ABCD là hình chữ nhật)
\(AD\subset\left(SAD\right)\)
BC không nằm trong mp(SAD)
Do đó: BC//(SAD)
c: AB//CD(ABCD là hình chữ nhật)
\(CD\subset\left(SCD\right)\)
AB không nằm trong mp(SCD)
Do đó: AB//(SCD)
d: Xét ΔSAC có
O,H lần lượt là trung điểm của CA,CS
=>OH là đường trung bình
=>OH//SA
OH//SA
\(SA\subset\left(SAB\right)\)
OH không nằm trong mp(SAB)
Do đó: OH//(SAB)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
6 tháng 12 2023
a/
Xét tg SAD có
SM=DM; SN=AN => MN là đường trung bình của tg SAD
=> MN//AD
Mà AD//BC (cạnh đối hbh)
=> MN//BC mà \(BC\in\left(SBC\right)\) => MN//(SBC)
C/m tương tự ta cũng có NP//(SCD)
b/
Ta có
NP//(SCD) (cmt) (1)
Xét tg SBD có
SP=BP (gt)
OB=OD (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> PO là đường trung bình của tg SBD
=> PO//SD mà \(SD\in\left(SCD\right)\) => PO//(SCD) (2)
Từ (1) và (2) => (ONP)//(SCD)
C/m tương tự ta cũng có (OMN)//(SBC)
c/
Trong (ABCD) , qua O dựng đường thẳng // AD cắt AB và CD lần lượt tại H và K Ta có
MN//AD (cmt)
=> KH//MN
\(O\in\left(OMN\right);O\in KH\)
\(\Rightarrow KH\in\left(OMN\right)\) mà \(H\in AB;K\in CD\)
=>K; H là giao của (OMN) với CD và AB
d/
Ta có
KH//AD
AB//CD => AH//DK
=> AHKD là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> AD=HK
Ta có
MN là đường trung bình của tg SAD (cmt)
\(\Rightarrow MN=\dfrac{AD}{2}\) mà AD=HK (cmt)
\(\Rightarrow MN=\dfrac{HK}{2}\Rightarrow\dfrac{MN}{HK}=\dfrac{1}{2}\)
a: ABCD là hình chữ nhật tâm O
=>O là trung điểm chung của AC và BD
Xét ΔASC có
O,E lần lượt là trung điểm của AC,AS
=>OE là đường trung bình
=>OE//SC
mà SC\(\subset\left(SCD\right)\) và OE không thuộc (SCD)
nên OE//(SCD)
b: Xét ΔBSD có
\(\dfrac{BO}{BD}=\dfrac{BF}{BS}=\dfrac{1}{2}\)
nên OF//SD
=>OF//(SDC)
c: OE//(SDC)
OF//(SDC)
\(OE,OF\subset\left(OEF\right)\)
Do đó: (OEF)//(SCD)