Cho hình vuông ABCD. Dựng điểm E nằm trong hình vuông ABCD sao cho tam giác ABE đều, điểm F nằm ngoài hình vuông ABCD sao cho tam giác FBC đều.
Chứng minh rằng D, E, F thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 10 2017
a, Trong hình vuông ABCD dựng tam giác EMB đều.
MBA^=ABC^−CBE^−EBM^=90o−15o−60o=15oMBA^=ABC^−CBE^−EBM^=90o−15o−60o=15o
Dễ dàng c/m đc:
ΔΔ CEB=ΔΔ BMA (c.g.c)
\RightarrowBMA^=BEC^=150oBMA^=BEC^=150o
\RightarrowBMA^=EMA^=150oBMA^=EMA^=150o
\Rightarrow
ΔΔ EMA=ΔΔ BMA (c.g.c)
\Rightarrow AE=AB
Tương tự c/m đc DE=DC
\Rightarrow DE=AE(1)
Dễ dàng c/m đc DAE^=60o(2)DAE^=60o(2)
Từ (1) và (2) \Rightarrow Tam giác AED đều.
11 tháng 3 2021
Do tam giác FCD đều nên FC = DC = CB. Do đó tam giác BCF cân tại C nên \(\widehat{FBC}=\dfrac{180^o-\widehat{FCB}}{2}=\dfrac{180^o-150^o}{2}=15^o=\widehat{EBC}\).
Vậy B, E, F thẳng hàng.
11 tháng 3 2021
Trúc Giang Bạn cần giải thích đoạn nào vậy?
Tam giác BCF cân tại C nên \(\widehat{FBC}=\widehat{BFC}\).
Do đó \(\widehat{FBC}+\widehat{BFC}+\widehat{FCB}=180^o\Leftrightarrow\widehat{FCB}+2\widehat{FBC}=180^o\Leftrightarrow\widehat{FBC}=\dfrac{180^o-\widehat{FCB}}{2}\).
Do đó \(\widehat{FBC}=\widehat{EBC}\) mà E, F cùng thuộc 1 nửa mf bờ BC nên E, B, F thẳng hàng.
CM
27 tháng 7 2017
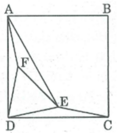
Xét ∆ EDC và ∆ FDA, tacó: ∠ (EDC) = ∠ (FDA) = 15 0
DC = AD (gt)
∠ (ECD) = ∠ (FAD) = 15 0
Suy ra: ∆ EDC = ∆ FDA (g.c.g)
⇒ DE = DF
⇒ ∆ DEF cân tại D
Lại có: ∠ (ADC) = ∠ (FDA) + ∠ (FDE) + ∠ (EDC)
⇒ ∠ (FDE) = ∠ (ADC) -( ∠ (FDA) + ∠ (EDC) )= 90 0 - ( 15 0 + 15 0 ) = 60 0
Vậy ∆ DEF đều.
HC
3 tháng 9 2020
Bài giải
Ta có \(\widehat{DAE}=90^0-60^0=30^0\)
\(AD=AE(=AB) \)
\(\Rightarrow \triangle DAE\)cân tại A
\(\widehat{EDA}=\frac{180^0-30^0}{2}=75^0
\)
Nên \(\widehat{CDE}=15^0\)
Tương tự \(\triangle BEC\) cân tại \(B\)
Dễ chứng minh \(\triangle DAF=\triangle DCF\) (c.g.c)
\(\Rightarrow \widehat{DFC}=\widehat{DFA}=180^0-45^0-30^0=105^0\)
Hạ \(FH \perp DC\)
Thì dễ có \(\triangle DHF\) vuông cân tại \(H\)
\(\Rightarrow \widehat{ DFH}=45^0\) do đó \(HD=HO\)
\(\Rightarrow \widehat{HFC}=60^0\)
Tam giác \(HFC\) vuông tại \(H\) có \(\widehat{HFC}=60^0\)
Giả sử \(O'\) \)là trung điểm của\( FC\) thì \(\triangle HO'F\)đều
\(\Rightarrow HO'=HF=DH\)
\(\widehat{HDO'}=\frac{180^0-(60^0+90^0)}{2}=15^0=\widehat{CDE}\)
Nên\( D, E, O'\)thẳng hàng \(\Rightarrow O\) trùng \(O' \)
Hay\(O\) là trung điểm của \(CF\) nên \(OC=OF\)
vì tam giác ABE đều nên góc ABE = AEB = 600
suy ra goc EBC = 90 - 30 = 600
vì tam giác BFC đều nên goc FBC = FCB = 60o
Ta có tam giác EBF cân tại B (vì BE =BF ) và goc EBF = EBC + CBF = 60+30 = 90o
suy ra goc BEF = \(\frac{180-90}{2}\)=45o
ta có goc AEF = AEB + BEF = 60 + 45 = 105o
ta có tam giac AED cân tại A(vì AD = AE) và goc EAD = 30o nên goc AED = \(\frac{180-30}{2}\)= 75o
Ta có goc AED + goc AEF = 75 + 105 = 180o
suy ra D, E, F thẳng hàng