theo cách lớp 9 nhé.cảm ơn ạ
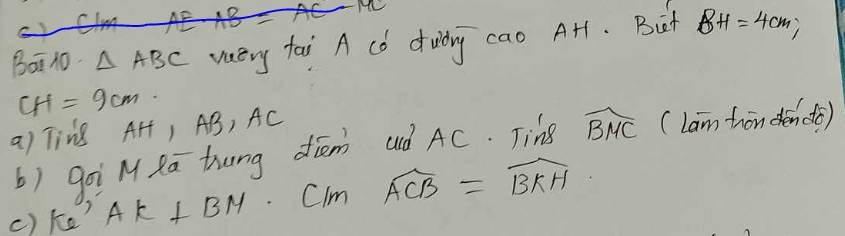
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3.
\(\Delta'=\left(m-1\right)^2-\left(-2m-1\right)=m^2+2>0;\forall m\)
\(\Rightarrow\) Pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-2m-1\end{matrix}\right.\)
\(2x_1+3x_2+3x_1x_2=-11\)
\(\Leftrightarrow2\left(x_1+x_2\right)+x_2+3x_1x_2=-11\)
\(\Leftrightarrow4\left(m-1\right)+x_2+3\left(-2m-1\right)=-11\)
\(\Leftrightarrow x_2=2m-4\)
Thế vào \(x_1+x_2=2\left(m-1\right)\)
\(\Rightarrow x_1=2\left(m-1\right)-\left(2m-4\right)=2\)
Thế \(x_1=2;x_2=2m-4\) vào \(x_1x_2=-2m-1\)
\(\Rightarrow2\left(2m-4\right)=-2m-1\)
\(\Rightarrow m=\dfrac{7}{6}\)
4.
\(\Delta'=\left(m+1\right)^2-\left(m^2-m-5\right)=3m+6>0\Rightarrow m>-2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2\left(m+1\right)\\x_1x_2=m^2-m-5\end{matrix}\right.\)
Do \(x_1\) là nghiệm của pt nên:
\(x_1^2+2\left(m+1\right)x_1+m^2-m-5=0\)
\(\Rightarrow x_1^2=-2\left(m+1\right)x_1-m^2+m+5\)
Từ đó ta được:
\(x_1^2-2\left(m+1\right)x_2+m^2-m-5=16\)
\(\Leftrightarrow-2\left(m+1\right)x_1-m^2+m-5-2\left(m+1\right)x_2+m^2-m-5=16\)
\(\Leftrightarrow-2\left(m+1\right)\left(x_1+x_2\right)=16\)
\(\Leftrightarrow4\left(m+1\right)^2=16\)
\(\Leftrightarrow\left(m+1\right)^2=4\)
\(\Rightarrow\left[{}\begin{matrix}m+1=2\\m+1=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=1\\m=-3< -2\left(loại\right)\end{matrix}\right.\)

5.
\(\Delta=m^2-4\left(m-1\right)=\left(m-2\right)^2\)
Pt có 2 nghiệm pb khi \(\left(m-2\right)^2>0\Rightarrow m\ne2\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=x_1+x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=x_1+x_2\)
\(\Leftrightarrow m^2-2\left(m-1\right)=m\)
\(\Leftrightarrow m^2-3m+2=0\Rightarrow\left[{}\begin{matrix}m=1\\m=2\left(loại\right)\end{matrix}\right.\)
1.
\(\Delta=9+4m>0\Rightarrow m>-\dfrac{9}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=-m\end{matrix}\right.\)
\(5x_1+5x_2=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5\left(x_1+x_2\right)=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5.\left(-3\right)=1-\left(-m\right)^2\)
\(\Leftrightarrow m^2=16\Rightarrow\left[{}\begin{matrix}m=4\\m=-4< -\dfrac{9}{4}\left(loại\right)\end{matrix}\right.\)
2.
\(\Delta=\left(2m+1\right)^2-4\left(m^2+1\right)=4m-3>0\Rightarrow m>\dfrac{3}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+1\\x_1x_2=m^2+1\end{matrix}\right.\)
\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=13\)
\(\Leftrightarrow x_1^2+2x_1+1+x_2^2+2x_2+1=13\)
\(\Leftrightarrow x_1^2+x_2^2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(2m+1\right)^2-2\left(m^2+1\right)+2\left(2m+1\right)=11\)
\(\Leftrightarrow2m^2+8m-10=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-5< \dfrac{3}{4}\left(loại\right)\end{matrix}\right.\)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: Xét ΔABC vuông tại A có AM là đường cao
nên \(\left\{{}\begin{matrix}AB\cdot AC=AM\cdot BC\\AB^2=BM\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AM=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\\BM=\dfrac{12^2}{20}=7.2\left(cm\right)\end{matrix}\right.\)
c: ΔABM vuông tại M có ME là đường cao
nên \(AE\cdot AB=AM^2\)
ΔAMC vuông tại M
=>\(MA^2+MC^2=AC^2\)
=>\(MA^2=AC^2-MC^2\)
=>\(AE\cdot AB=AC^2-MC^2\)

a: ΔAMN vuông tại A
mà AI là đường trung tuyến
nên AI=IM=IN=MN/2
=>I là tâm đường tròn ngoại tiếp ΔAMN
b: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E

1.would met -> meet
2.B.he-> who
3.watching -> watch
4.more happier-> bỏ more
5. is planted -> was planted
6. boring -> bored
7. which -> where
8. many -> any
9. good -> best
10. learning -> to learn

Bài 3:
Nếu đáy lớn được tăng thêm 5 cm thì diện tích sẽ tăng một phần bằng 5 x chiều cao : 2
Vậy chiều cao của hình thang là:
$20\times 2:5=2$ (m)
Diện tích hình thang ban đầu là:
$50\times 2:2=50$ (m2)

Hình như là:
Headache : Đau đầu
Stomachache: Đau bụng
Temperature:Nhiệt độ
Earache: Đau tai
Sore throat: Đau cổ họng
Sore Eyes:Đau mắt
Cold:Cảm lạnh
a: BC=BH+CH
=4+9
=13(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=\sqrt{4\cdot9}=6\left(cm\right)\\AB=\sqrt{4\cdot13}=2\sqrt{13}\left(cm\right)\\AC=\sqrt{9\cdot13}=3\sqrt{13}\left(cm\right)\end{matrix}\right.\)
b: AM=AC/2=1,5*căn 13(cm)
Xét ΔAMB vuông tại M có
\(\tan AMB=\dfrac{AB}{AM}=\dfrac{2\sqrt{13}}{1.5\sqrt{13}}=\dfrac{4}{3}\)
=>\(\widehat{AMB}\simeq53^0\)
=>\(\widehat{BMC}=180^0-53^0=127^0\)
c: Xét tứ giác AKHB có \(\widehat{AKB}=\widehat{AHB}=90^0\)
nên AKHB là tứ giác nội tiếp
=>\(\widehat{BKH}=\widehat{BAH}\)
mà \(\widehat{BAH}=\widehat{C}\)
nên \(\widehat{BKH}=\widehat{C}\)
có thể vẽ hình giúp e đc k ạ?