Question

[Thầy Cao Đô]

Bài 4. (0,5 điểm) Từ hai vị trí $A$ và $B$ của một tòa nhà, người ta quan sát đỉnh $C$ của ngọn núi.

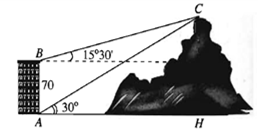
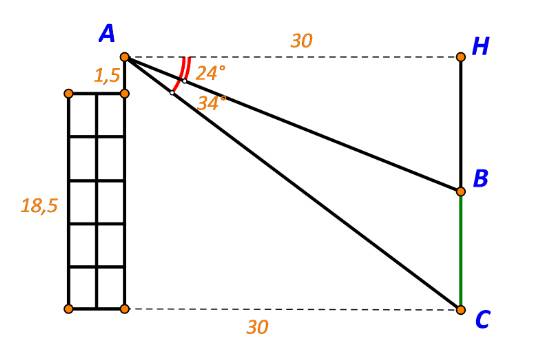
Biết rằng độ cao $AB=70$ m, phương nhìn $AC$ tạo với phương nằm ngang góc ${{30}^{\circ}}$, phương nhìn $BC$ tạo với phương nằm ngang góc ${{15}^{\circ}}30'$ (tham khảo hình vẽ trên). Ngọn núi đó có độ cao so với mặt đất là bao nhiêu mét?

Answer 1

[Bùi Kiên Cường]

 

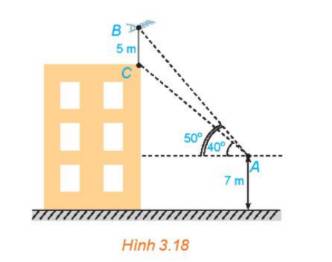
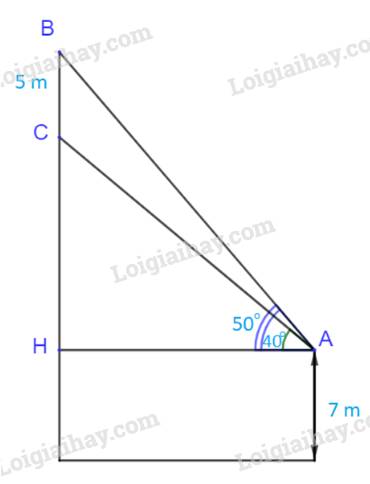
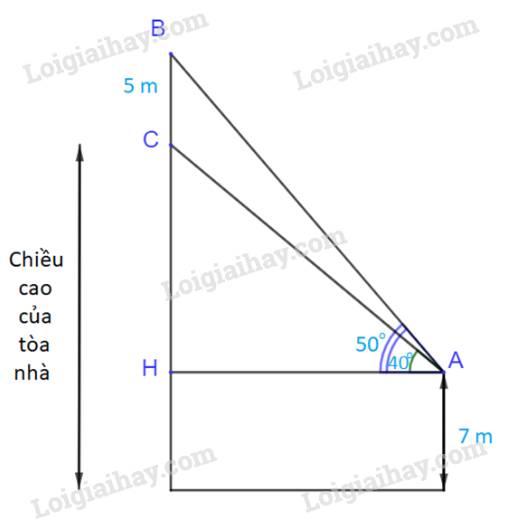
$\widehat{ABC}=90°+15°30\text{'}=105°30\text{'}$ 

Xét tam giác ABC có $\widehat{CAB}=60°,\widehat{ABC}=105°30\text{'}$ ta có: 

$\widehat{CAB}+\widehat{ABC}+\widehat{ACB}=180°$ (định lí tổng ba góc trong tam giác)

$\Rightarrow \widehat{ACB}=180°-\widehat{CAB}-\widehat{ABC}$ 

$\Rightarrow \widehat{ACB}=180°-60°-105°30\text{'}=14°30\text{'}.$

Áp dụng định lí sin trong tam giác ABC, ta có: $\frac{AC}{\sin \widehat{ABC}}=\frac{AB}{\sin \widehat{ACB}}$

$\Rightarrow AC=\frac{AB.\sin \widehat{ABC}}{\sin \widehat{ACB}}=\frac{70.\sin 105°30\text{'}}{\sin 14°30\text{'}}\approx 269,4\left(m\right)$

Answer 2

[Trần Lê Thanh Thảo]