1 cái loa có công suất 0,02 mW khi mở hết công suất . Tính cường độ âm tại điểm cách loa 10m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cường độ âm I' ứng với mức 70 dB hay 7 B là :
I ' = 10 I 0 = 10 7 . 10 - 12 = 10 - 5 w / m 2
Vây phải giảm nhỏ công suất của loa : N = 5. 10 - 3 / 10 - 5 = 500 lần.

Tại điểm cách loa 1m ta có \(R=1m\)
Cường độ âm có độ lớn:
\(I=\dfrac{P}{4\pi R^2}=\dfrac{1}{4\pi\cdot1^2}=\dfrac{1}{4\pi}\approx0,08W/m^2\)

Đáp án C
Cường độ âm do các loa truyền đến điểm M :
I M = ( I N + I N ' ) ≡ P 2 π 1 a 2 + b 2 4 + 1 a 2 + b 2 4 + h 2
Để IM là lớn nhất thì biểu thức dưới mẫu phải nhỏ nhất. Ta có :
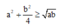 dấu bằng xảy ra khi
a
=
b
2
⇒
a
=
3
b
=
6
dấu bằng xảy ra khi
a
=
b
2
⇒
a
=
3
b
=
6
Giá trị cường độ âm khi đó
( I M ) m a x = 5 P m a x 108 π = 10
⇒ P m a x = 678 W


C ó f ' t = 2 t + 16 2 t + 16 - t 2 + 16 t 2 2 t + 16 2 = 2 t 2 + 32 t + 256 2 t + 16 2 > 0 ∀ t
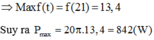

Đáp án A
Ta có : 2 B C - A B ≤ 2 m
Mặt khác : B C . A B = 20 m (1)
Công suất lớn nhất khi B C m a x ⇒ 2 B C - A B = 2 m (2)
Từ (1) và (2) suy ra : B C ≈ 3 , 7 m ; A B ≈ 5 , 4 m
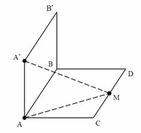
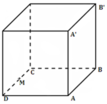
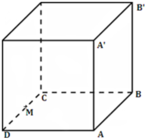
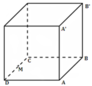
Dễ dàng tính được : AM = 4,58m và A’M = 6,08m
Tại người nghe được âm có mức cường độ âm lớn nhất là 13(B) = 130(dB)
⇒ 13 = log ( 2 P 4 π A M 2 I 0 + 2 P 4 π A ' M 2 I 0 ) ⇒ P = 840 , 9 ( W ) .
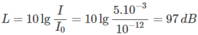


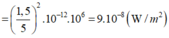


Cường độ âm:
\(I=\dfrac{P}{4\pi r^2}=\dfrac{0,02\cdot10^{-3}}{4\pi\cdot10^2}=1,6\cdot10^{-8}W/m^2\)