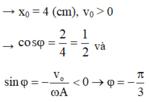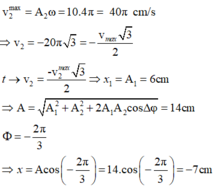Vật dao động điều hoà, biết khi pha dao động là 2π/3 thì vật có li độ là - 4cm và gia tốc 16 cm/s2. Lập phương trình dao động, chọn gốc thời gian lúc vật có li độ 4√2 cm và đang chuyển động theo chiều âm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(Acos\left(\omega t=\varphi\right)\)
\(v=-A\omega sin\left(\omega t+\varphi\right)\)
\(a=-A\omega^2cos\left(\omega t+\varphi\right)\)
t = 0
\(x=Acos\varphi=-\sqrt{2}\)
\(v=-A\omega sin\varphi=-\pi\sqrt{2}\)
\(a=-A\omega^2cos\varphi=\pi^2\sqrt{2}\)
Lấy a chia cho x ta được \(\omega=\frac{\pi rad}{s}\)
v chia cho a ta được \(tan\varphi=-1\) mà cos góc này nhỏ hơn 0 nên \(\varphi=\frac{3\pi}{4}\)
A=2cm
Vậy \(x=2cos\left(\pi t+\frac{3\pi}{4}\right)cm\)

Chọn đáp án D
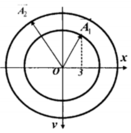
Tại t: dao động thứ hai có vận tốc là:
− 20 π 3 c m / s = − V 2 max 2 . 3 cm/s
và tốc độ đang giảm nên tại t pha dao động thứ 2 là 2π/3 rad.
Mà x1 và x2 lệch pha nhau π/3 suy ra tại t thì pha của x1 là π/3.
Suy ra A 1 = 3.2 = 6 cm.
A = A 1 2 + A 2 2 + 2 A 1 A 2 cos φ = 6 2 + 10 2 + 2.6.10. cos π 3 = 14 c m
Suy ra khi pha dao động tổng hợp là − 2 π 3 thì li độ dao động tổng hợp là:
x = A . cos − 2 π 3 = − 7 c m .

Đáp án D
Chu kì dao động
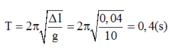
Trong một chu kì dao động, thời gian lò xo bị nén là khoảng thời gian vật đi từ x = ∆l đến x = A rồi trở về x = ∆l, tức là ∆t = 2t0 với t0 là thời gian đi từ x = ∆l đến x = A (giả sử chiều dương của trục tọa độ hướng lên).
Theo giả thiết:
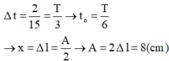
Khi lò xo giãn 8 cm ![]() vật đang chuyển động chậm dần đều nên đang đi ra biên, đi theo chiều dương hướng xuống
vật đang chuyển động chậm dần đều nên đang đi ra biên, đi theo chiều dương hướng xuống