Thay dấu “?” bằng số thích hợp trong bảng sau:

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


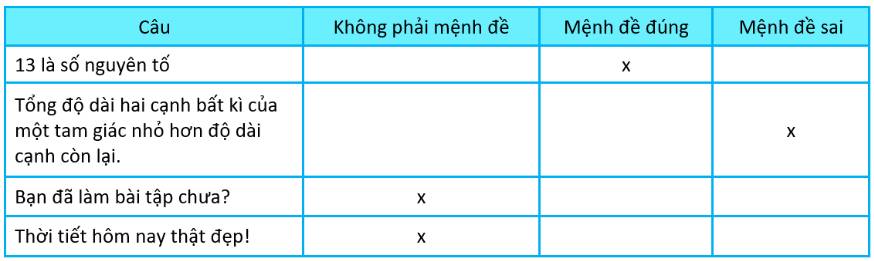
“13 là số nguyên tố” là mệnh đề đúng.
“Tổng độ dài hai cạnh bất kì của một tam giác nhỏ hơn độ dài cạnh còn lại.” là mệnh đề sai.
(Giải thích: Vì theo bất đẳng thức tam giác: Trong một tam giác bất kỳ, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.)
“Bạn đã làm bài tập chưa?”: không phải mệnh đề.
(Giải thích: Đây là câu hỏi, không xác định được tính đúng sai.)
“Thời tiết hôm nay thật đẹp!”: không phải mệnh đề.
(Giải thích: Đây là câu cảm thán, không xác định được tính đúng sai.)
Chú ý khi giải:
+ Thông thường, các câu khẳng định có thể xác định tính đúng sai.
+ Còn các câu nghi vấn, câu cảm thán, câu cầu khiến thì không xác định được tính đúng sai nên không là mệnh đề.

Vì x và y là hai đại lượng tỉ lệ nghịch nên xy = a (với a là một số khác 0).
Khi x = 2, y = 15 ⇒ a = xy = 30
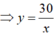
Vì x và y là hai đại lượng tỉ lệ nghịch nên:
x1.y1 = x2.y2 = x3. y3 = x4.y4 = 30.
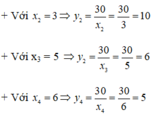
Kết quả như sau:
| x1 = 2 | x2 = 3 | x3 = 5 | x4 = 6 |
| y1 = 15 | y2 = 10 | y3 = 6 | y4 = 5 |
| x1y1 = 30 | x2y2 = 30 | x3y3 = 30 | x4y4 = 30 |

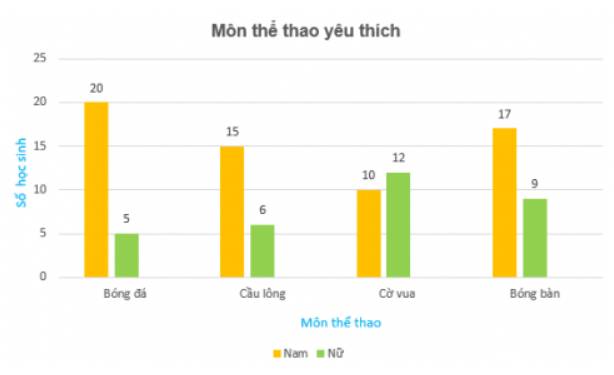
Trục nằm ngang biểu diễn các môn thể thao, với mỗi môn thể thao có 2 cột, cột màu cam biểu diễn cho số nam và cột màu xanh biểu diễn cho số nữ.

Môn bóng đá: Nam có 20 và nữ có 5 nên ta điền số trên cột màu cam là 20 và số trên cột màu xanh là 5.
Tương tự với môn cầu lông, cờ vua và bóng bàn.

a | b | 3 | c | d | e | f | g | h | -4 | i |
+) Ta có: 3.c.d = 60 nên c.d=20
Mà c.d.e=60 nên 20.e=60 hay e=3
+) Tương tự, 3.f.g=60 nên f.g=20
Mà f.g.h=60 nên 20.h=60 hay h = 3
+) Vì h.(-4).i = 60 nên 3.(-4).i = 60 nên i = -5
+) Vì g.h.(-4) = 60 nên g.3.(-4) = 60 nên g = -5
+) Vì f.g=20 nên f.(-5) = 20 hay f = -4
Ta có:
d.e.f = 60 nên d.3.(-4) = 60 nên d = -5
3.c.d = 60 nên 3.c.(-5) =60 nên c =-4
a.b.3 = b.3.c nên a = c
b.3.c = 3.c.d nên b = d
Ta được:
-4 | -5 | 3 | -4 | -5 | 3 | -4 | -5 | 3 | -4 | -5 |

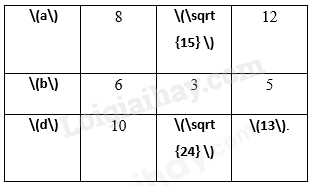
Giả sử \(ABCD\) là hình chữ nhật ; \(a\), \(b\), \(d\) lần lượt là độ dài của \(AB\), \(BC\), \(AC\)
Áp dụng định lý Pythagore vào \(\Delta ABC\) vuông tại \(B\) ta có:
\(A{C^2} = A{B^2} + B{C^2}\)
Do đó \({d^2} = {a^2} + {b^2}\) ; \({b^2} = {d^2} - {a^2}\); \({a^2} = {d^2} - {b^2}\)
Suy ra: \(d = \sqrt {{a^2} + {b^2}} \); \(b = \sqrt {{d^2} - {a^2}} \); \(a = \sqrt {{d^2} - {b^2}} \)
Với \(a = 8\); \(b = 6\) ta có: \(d = \sqrt {{8^2} + {6^2}} = \sqrt {64 + 36} = \sqrt {100} = 10\)
Với \(a = \sqrt {15} \); \(d = \sqrt {24} \) ta có: \(b = \sqrt {{{\sqrt {24} }^2} - {{\sqrt {15} }^2}} = \sqrt {24 - 15} = \sqrt 9 = 3\)
Với \(b = 5\); \(d = 13\) ta có: \(a = \sqrt {{{13}^2} - {5^2}} = \sqrt {169 - 25} = \sqrt {144} = 12\)

Tham khảo:
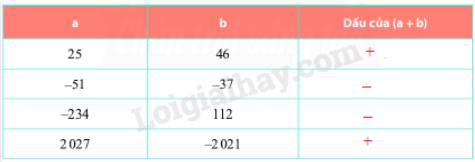
\(a = 25;b = 46\), tức là a và b cùng mang dấu (+) nên \(a + b\) mang dấu (+)
\(a = - 51;b = - 37 \Rightarrow \) a và b cùng mang dấu \(\left( - \right)\) nên \(a + b\) mang dấu \(\left( - \right)\)
Số đối của \(\left( { - 234} \right)\) là \(234 > 112\) nên \(a + b\) mang dấu \(\left( - \right)\)
Số đối của \(\left( { - 2021} \right)\) là 2021 < 2 027 nên \(a + b\) mang dấu (+)
Ta được bảng:

a/
Vì z và y là 2 đại lượng tỉ lệ nghịch nên
=>x.y=a
=>2.30=a
=>a=60
Vậy x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ là 60.
b/
y2=20
y3=15
y4=12
+) Với \(a = \dfrac{9}{{25}},b = 1\) thì \(a.b = \dfrac{9}{{25}}.1 = \dfrac{9}{{25}}\)
\(a:b = \dfrac{9}{{25}}:1 = \dfrac{9}{{25}}\)
+) Tương tự với \(a = 12,b = \dfrac{{ - 9}}{8}\) thì
\(\begin{array}{l}a.b = 12.\dfrac{{ - 9}}{8} = \dfrac{{12.\left( { - 9} \right)}}{{.8}} = \dfrac{{ - 27}}{2}\\a:b = 12:\dfrac{{ - 9}}{8} = 12.\dfrac{8}{{ - 9}} = \dfrac{{12.8}}{{ - 9}} = \dfrac{{ - 32}}{3}\end{array}\)
+) Với \(a = \dfrac{{ - 5}}{6},b = 3\) thì
\(\begin{array}{l}a.b = \dfrac{{ - 5}}{6}.3 = \dfrac{{ - 5}}{2}\\a:b = \dfrac{{ - 5}}{6}:3 = \dfrac{{ - 5}}{6}.\dfrac{1}{3} = \dfrac{{ - 5}}{{18}}\end{array}\)
Vậy ta có: