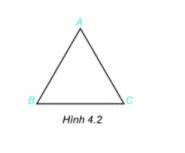
Cho tam giác đều ABC như hình 4.2.
1. Gọi tên các đỉnh, cạnh góc của tam giác đều ABC.
2. Dùng thước thẳng để đo và so sánh các cạnh của tam giác ABC.
3. Sử dụng thước đo góc để đo và so sánh các góc của tam giác ABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Các đỉnh: A, B, C, D
Các cạnh: AB, BC, CD, DA
Các đường chéo: AC, BD
2) Độ dài các cạnh của hình vuông đều bằng nhau
Độ dài 2 đường chéo của hình vuông bằng nhau
3) Các góc của hình vuông đều bằng nhau và bằng 90o

1) Đỉnh: A, B, C, D
Cạnh: AB, BC, CD, DA
Đường chéo: AC, BD
Hai cạnh đối: AB và CD; BC và AD
2) Ta đo được: \(\widehat{A} = 90^0; \widehat{B} = 90^0; \widehat{C} = 90^0; \widehat{D} = 90^0\). Vậy các góc của hình chữ nhật đều bằng nhau và bằng 90o
3) Ta đo được: AB = CD ; AD = BC nên hai cạnh đối của hình chữ nhật bằng nhau
AC = BD nên hai đường chéo của hình chữ nhật bằng nhau.

a.
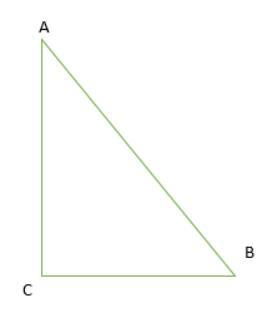
Góc CAB có số đo là 40 độ
Góc ABC có số đo là 50 độ
Góc ACB có số đo là 90 độ
b. Tổng ba góc trong tam giác là: 180 độ bằng với kết quả của các bạn khác.

c) Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{B}+\widehat{C}=180^0-40^0=140^0\)
Ta có: \(\widehat{B}:\widehat{C}=3:4\)(gt)
nên \(\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}\)
mà \(\widehat{B}+\widehat{C}=140^0\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}=\dfrac{\widehat{B}+\widehat{C}}{3+4}=\dfrac{140^0}{7}=20^0\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{\widehat{B}}{3}=20^0\\\dfrac{\widehat{C}}{4}=20^0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{B}=60^0\\\widehat{C}=80^0\end{matrix}\right.\)
Xét ΔABC có \(\widehat{A}< \widehat{B}< \widehat{C}\left(40^0< 60^0< 80^0\right)\)
mà cạnh đối diện với \(\widehat{A}\) là cạnh BC
cạnh đối diện với \(\widehat{B}\) là cạnh AC
và cạnh đối diện với \(\widehat{C}\) là cạnh AB
nên BC<AC<AB

a) Ghép 6 tam giác đều thành hình mới.
b) Hình vừa nhận được có các góc bằng nhau, các cạnh bằng nhau.
Đây là hình lục giác đều.


1: góc C=90-36=54 độ
góc B<góc C<góc A
=>AC<AB<BC
2: Xét ΔIAC và ΔIBE co
IA=IB
góc AIC=góc BIE
IC=IE
=>ΔIAC=ΔIBE
3: Xét ΔKAB có
KI vừa là đường cao, vừa là trung tuyến
=>ΔKAB cân tại K
=>góc KAB=góc KBA
=>góc KAC=góc KCA
=>KA=KC=KB
=>K là trung điểm của BC

a) Xét t/g ABD và t/g HBD có:
AB = BH (gt)
ABD = HBD ( vì BD là phân giác ABC)
BD là cạnh chung
Do đó, t/g ABD = t/g HBD (c.g.c)
=> BAD = BHD = 90o (2 góc tương ứng)
=> DH _|_ BC (đpcm)
b) t/g ABD = t/g HBD (câu a)
=> ADB = HDB (2 góc tương ứng)
Mà ADB + HDB = ADH = 110o
Do đó, ADB = HDB = 110o : 2 = 55o
t/g ABD vuông tại A có: ABD + ADB = 90o
=> ABD + 55o = 90o
=> ABD = 90o - 55o = 35o
k nhé
1) Các đỉnh : A, B, C
Các cạnh: AB, BC, AC
Các góc: \(\widehat A,\,\widehat B,\,\widehat C\)
2) AB =3 cm, AC = 3 cm, BC = 3 cm nên các cạnh của tam giác ABC bằng nhau
3) \(\widehat A = 60^0; \widehat B =60^0; \widehat C=60^0\) nên các góc của tam giác ABC bằng nhau và bằng 60o