Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km. Tại cùng một thời điểm, hai trạm cùng phát tín hiệu với vận tốc 292 000 km/s để một tàu thuỷ thu và đo độ lệch thời gian. Tín hiệu từ A đến sớm hơn tín hiệu từ B là 0,0005 s. Từ thông tin trên, ta có thể xác định được tàu thuỷ thuộc đường hypebol nào? Viết phương trình chính tắc của hypebol đó theo đơn vị kilômét.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là vị trí phát ra âm thanh cầu cứu trong rừng.
Gọi \({t_1},{t_2}\)lần lượt là thời gian trạm A, B nhận được tín hiệu cầu cứu (đơn vị: giây)
\( \Rightarrow {t_A} = {t_B} - 6 \Leftrightarrow {t_B} - {t_A} = 6\)
Đổi \(v = 1{\rm{ }}236{\rm{ }}km/h{\rm{ }} = \frac{{\;1236}}{{3600}}km/s = \frac{{103}}{{300}}km/s.\;\)
Ta có: \(MA = {t_A}.v;MB = {t_B}.v\)
\( \Rightarrow MB - MA = ({t_B} - {t_A}).v = 6.\frac{{103}}{{300}} = 2,06(km)\)
Như vậy, tập hợp các điểm M là một hypepol nhận A, B làm hai tiêu điểm.
Ta có: \(AB = 16 = 2c \Rightarrow c = 8\); \(\left| {MA - MB} \right| = 2,06 = 2a \Rightarrow a = 1,03\)
\( \Rightarrow {b^2} = {c^2} - {a^2} = {8^2} - 1,{03^2} = 62,9391\)
Vậy phương trình chính tắc của hypebol đó là: (H) \(\frac{{{x^2}}}{{1,0609}} - \frac{{{y^2}}}{{62,9391}} = 1\)
Do MA < MB nên M thuộc của nhánh (H) gần A.
Vậy phạm vi tìm kiếm vị trí phát ra âm thanh đó là nhánh gần A của hypebol (H) có phương trình \(\frac{{{x^2}}}{{1,0609}} - \frac{{{y^2}}}{{62,9391}} = 1\).

Gọi J là vị trí âm thanh phát đi. Ta có J cách đều O, A, B. Do đó J là giao của hài đường trun trực \({d_1},{d_2}\) tương ứng của OA, OB. Đường thẳng \({d_1}\) đi qua trung điểm M của OA và vuông góc với OA. Ta có \(M\left( {\frac{1}{2};0} \right)\) và \(\overrightarrow {{n_{{d_1}}}} = \overrightarrow {OA} = \left( {1;0} \right)\).
Phương trình đường thẳng \({d_1}\) là \(1\left( {x - \frac{1}{2}} \right) + 0\left( {y - 0} \right) = 0 \Leftrightarrow x = \frac{1}{2}\).
Tương tự, phương trình đường thẳng \({d_2}\) là \(x + 3y - 5 = 0\).
Tọa độ điểm J là nghiệm của hệ \(\left\{ \begin{array}{l}x = \frac{1}{2}\\x + 3y - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\y = \frac{3}{2}\end{array} \right.\).
Vậy \(J\left( {\frac{1}{2};\frac{3}{2}} \right)\).

Bình phương hai vế ta được:
\(\begin{array}{l}{(8 - 40x)^2} + {(7 - 40x)^2} = 25\\ \Leftrightarrow 64 - 640x + 1600{x^2} + 49 - 560x + 1600{x^2} = 25\\ \Leftrightarrow 3200{x^2} - 1200x + 88 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{{11}}{{40}}\\x = \frac{1}{{10}}\end{array} \right.\end{array}\)
Vậy phương trình có hai nghiệm là \(x = \frac{{11}}{{40}}\) và \(x = \frac{1}{{10}}\).

9. Trên một đường thẳng, tại hai điểm A và B cách nhau 10 km, có hai ô tô xuất phát cùng lúc và chuyển động cùng chiều. Ô tô xuất phát từ A có tốc độ 60 km/h và ô tô xuất phát từ B có tốc độ 40 km/h.
a) Lấy gốc tọa độ ở A, gốc thời gian là lúc xuất phát, hãy viết công thức tính quãng đường đi được và phương trình chuyển động của hai xe.
b) Vẽ đồ thị tọa độ - thời gian của hai xe trên cùng một hệ trục (x, t).
c) Dựa vào đồ thị tọa độ - thời gian để xác định vị trí và thời điểm mà xe A đuổi kịp xe B.
Trả lời:
![]()
a) Chọn gốc tọa độ ở A (O ≡ A); gốc thời gian là lúc xuất phát, chiều dương hướng từ A → B, trục Ox trùng với AB.
Ta có phương trình chuyển động thẳng đều của một chất điểm: x = x0 + vt
Đối với xe A: xA = 60t (km/h) (1)
Đối với xe B: xB = 40t + 10 (km/h) (2)
b) Đồ thị
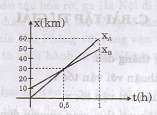
c) Khi xe A đuổi kịp xe B ta có: xA + xB
=> 60t = 40t + 10 => t = 0,5 h = 30 phút
Thay vào (1) => : xA = xB = x = 60 x 0,5 = 30 km
Vậy điểm đó cách A là 30km.
![]()
a) Chọn gốc tọa độ ở A (O ≡ A); gốc thời gian là lúc xuất phát, chiều dương hướng từ A → B, trục Ox trùng với AB.
Ta có phương trình chuyển động thẳng đều của một chất điểm: x = x0 + vt
Đối với xe A: xA = 60t (km/h) (1)
Đối với xe B: xB = 40t + 10 (km/h) (2)
b) Đồ thị

c) Khi xe A đuổi kịp xe B ta có: xA + xB
=> 60t = 40t + 10 => t = 0,5 h = 30 phút
Thay vào (1) => : xA = xB = x = 60 x 0,5 = 30 km
Vậy điểm đó cách A là 30km.

\(=>S1=50t\left(km\right)\) (qđ xe từ A)
\(=>S2=40t\left(km\right)\)(qđ xe từ B)
\(=>30+40t=50t=>t=3h\)
=>kể từ khi 2 xe xuất phát sau 3h thì gặp nhau
vị trí gặp nhau cách A \(Sa=S1=50.3=150km\)
Hai xe xuất phát cùng một lúc nên gọi thời gian chuyển động của hai xe là t
Gọi v1 là vận tốc của ô tô 1; v2 là vận tốc của ô tô 2
Xe đi từ A có đường đi là s1 = v1t = 40t
Hai xe chuyển động cùng chiều từ A đến B nên lúc đầu xe B cách A một đoạn s0 = 20km
Xe đi từ B cách A một đoạn đường là: s2 = s0 + v2t = 20 + 30t (km)
Khoảng cách giữa hai xe: Δs = s2 - s1 = 20 + 30t - 40t = 20 - 10t (km)

Quãng đường xe đi từ A đi được cho đến khi gặp xe đi từ B
Quãng đường xe đi từ B đi được cho đến khi gặp xe đi từ A
Khi hai xe gặp nhau ta có:
Hai xe gặp nhau sau kể từ lúc xuất phát
Nơi gặp nhau cách A 45km
Thời điểm hai xe cách nhau 40km
TH1 : Trước khi hai xe gặp nhau
Hai xe cách nhau 40km khi
TH2 : Sau khi hai xe gặp nhau
Hai xe cách nhau 40km khi
Sau 1h hoặc sau 2h thì hai xe cách nhau 40km

Chọn đáp án D
+ Thời gian sóng vô tuyến truyền từ trạm Rada đến mục tiêu là: Δt = 0 , 15 ms
+ Khoảng cách d = c . Δt =45000 m =45 km

Hai xe gặp nhau khi x A = x B . Từ đó suy ra :
- Thời điểm hai xe gặp nhau kể từ khi xuất phát : 80t = 20 + 40t
Hay t = 20/40 = 0.5(h)
- Vị trí hai xe gặp nhau cách A một đoạn : x A = 80.0,5 = 40 km.
Gọi M là vị trí tàu thu tín hiệu. Gọi \({t_A},{t_B}\) lần lượt là thời gian tín hiệu truyền từ trạm phát A,B đến M. Theo đề bài, ta có \({t_A} - {t_B} = - 0,0005s\).
Suy ra \(MA - MB = v.{t_A} - v.{t_B} = 292000.\left( { - 0,0005} \right) = - 146km\).
Gọi (H) là hyperbol ở dạng chính tắc nhận A,B làm hai tiêu điểm và đi qua M. Khi đó ta có:
\(\left\{ \begin{array}{l}2a = \left| {MA - MB} \right| = 146\\2c = AB = 300\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\c = 150\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\{b^2} = {c^2} - {a^2} = 17171\end{array} \right.\)
Vậy phương trình chính tắc của (H) là: \(\frac{{{x^2}}}{{5329}} - \frac{{{y^2}}}{{17171}} = 1\).