Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có: \(\overline{abcabc}=100000a+10000b+1000c+100a+10b+c\) \(=100100a+10010b+1001c\) \(=1001\left(100a+10b+c\right)=7\cdot11\cdot13\left(100a+10b+c\right)⋮7,11,13\)
b) Ta có: \(\overline{ab}-\overline{ba}=10a+b-10b-a=9a-9b\) \(=9\left(a-b\right)⋮9\)
c) Ta có: \(\overline{abc}-\overline{cba}=100a+10b+c-100c-10b-a=99a-99c=99\left(a-c\right)⋮99\)
Bài 1:
a)
\(\overline{abcd}=100\overline{ab}+\overline{cd}\)
\(=100.2\overline{cd}+\overline{cd}\)
\(=201\overline{cd}\)
Mà \(201⋮67\)
\(\Rightarrow\overline{abcd}⋮67\)
b)
\(\overline{abc}=100\overline{a}+10\overline{b}+\overline{c}\)
\(=\left(100\overline{b}+10\overline{c}+\overline{a}\right)+\left(99\overline{a}-90\overline{b}-9\overline{c}\right)\)
\(=\overline{bca}+9\left[\left(12\overline{a}-9\overline{b}\right)-\left(\overline{a}+\overline{b}+\overline{c}\right)\right]\)
\(=\overline{bca}+27\left(4\overline{a}-3\overline{b}\right)-\left(\overline{a}+\overline{b}+\overline{c}\right)⋮27\)
\(\Rightarrow\overline{bca}-\left(\overline{a}+\overline{b}+\overline{c}\right)⋮27\)
\(\Rightarrow\left\{{}\begin{matrix}\overline{bca}⋮27\\\overline{a}+\overline{b}+\overline{c}⋮27\end{matrix}\right.\)
\(\Rightarrow\overline{bca}⋮27\)
Bài 2:
\(\overline{abcd}=\overline{ab}.100+\overline{cd}\)
\(=\overline{ab}.99+\overline{ab}+\overline{cd}\)
\(=\overline{ab}.11.99+\left(\overline{ab}+\overline{cd}\right)\)
Mà \(11⋮11\)
\(\Rightarrow\overline{ab}.11.9⋮11\)
\(\Rightarrow\overline{abcd}⋮11\).
Đặt \(\overline{abc}=11m+k;\overline{xyz}=11n+k\left(k\in N,k< 11\right)\)
Khi đó ta có: \(\overline{abcxyz}=1000.\overline{abc}+\overline{xyz}=1000\left(11m+k\right)+11n+k\)
\(=11000m+11n+1001k\)
Biểu thức trên chia hết cho 11 với mọi m, n, k.
Vậy ....
Ta có: abcdeg = 1000abc + deg = 2000deg + deg = 2001deg
Vì 2001 chia hết cho 23 và 29 => 2001deg chia hết cho 23 và 29 => abcdeg chia hết cho 23 và 29
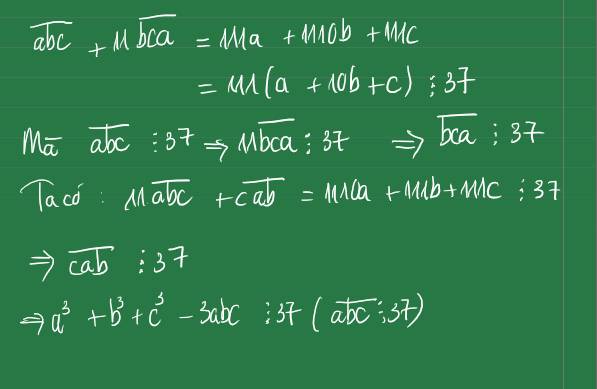
ai giúp mk mk tc cho 3 cái
C1 : Dấu hiệu chia hết cho 11 :
1 số chia hết cho 11 và chỉ khi tổng các số hàng chẵn / lẻ chia hết cho 11
Theo giả thiết /ab + /cd + /eg = 10a + b + 10c + d + 10e + g = 11. ( a + c + e ) + ( b +d + g ) - ( a + c + e ) chia hết cho 11
Suy ra : ( b + d + g ) - ( a + c + e ) chia hết cho 11
Suy ra abcdeg chia hết cho 11
C2 : Ta có
abcdeg = ab . 10000 = cd . 100 + eg
= ( 9999ab ) + ( 99cd )+ ( ab + cd + eg )
Vì 9999ab + 99cd chia hết cho 11 và ab + cd + eg chia hết cho 11
Suy ra : abcdeg chia hết cho 11
( cách nào cũng đúng nha )