Độ cao so với mặt đất của một quá bóng được ném lên theo phương thẳng đứng được mô tả bởi hàm số bậc hai \(h(t) = - 4,9{t^2} + 20t + 1\), ở độ cao \(h(t)\)tính bằng mét và thời gian t tình bằng giây. Trong khoảng thời điểm nào trong quá trình bay của nó, quả bóng sẽ ở độ cao trên 5m so với mặt đất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Theo giả thiết ta có bất phương trình sau: \( - 4,9{t^2} + 10t + 1,6 > 7 \Leftrightarrow - 4,9{t^2} + 10t - 5,4 > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 10t - 5,4\) có \(\Delta = - \frac{{146}}{{25}} < 0\) và \(a = - 4,9 < 0\)
nên \(f\left( x \right)\) âm với mọi t, suy ra bât phương trình \( - 4,9{t^2} + 10t + 1,6 > 7\) vô nghiệm
vậy bóng không thể cao trên 7 m
b) Theo giả thiết ta có bất phương trình sau: \( - 4,9{t^2} + 10t + 1,6 > 5 \Leftrightarrow - 4,9{t^2} + 10t - 3,4 > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 10t - 3,4\) có hai nghiệm phân biệt là \({t_1} \simeq 0,43;{t_2} \simeq 1,61\) và \(a = - 4,9 < 0\)
nên \(f\left( t \right)\) dương khi t nằm trong khoảng \(\left( {0,43;1,61} \right)\)
Vậy khi t nằm trong khoảng \(\left( {0,43;1,61} \right)\)giây thì bóng ở độ cao trên 5 m

Theo giả thiết, khoảng thời gian bóng nằm ở độ cao 40 m là nghiệm của bất phương trình sau:
\(\begin{array}{l}h\left( t \right) > 40 \Leftrightarrow - 4,9{t^2} + 30t + 2 > 40\\ \Leftrightarrow - 4,9{t^2} + 30t - 38 > 0\end{array}\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 30t - 38\) có \(\Delta = 155,2 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,8;{x_2} \simeq 4,3\) và có \(a = - 4,9 < 0\)
Ta có bảng xét dấu như sau:
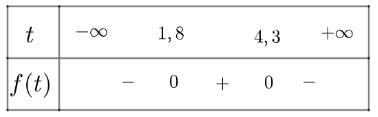
Từ đó cho thấy khoảng từ 1,8 s đến 4,3 s lag khoảng thời gian bóng cao so với mặt đất lớn hơn 40 m
Vậy quả bóng nằm ở độ cao trên 40 m trong thời gian 2,5 giây.

Với \({x_0}\) bất kì, ta có:
\(f'\left( {{t_0}} \right) = \mathop {\lim }\limits_{t \to {t_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{19,6t - 4,9{t^2} - 19,6{t_0} + 4,9t_0^2}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to {t_0}} \frac{{ - 4,9\left( {{t^2} - t_0^2} \right) + 19,6\left( {t - {t_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to {t_0}} \frac{{\left( {t - {t_0}} \right)\left( { - 4,9t - 4,9{t_0} + 19,6} \right)}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to {t_0}} \left( { - 4,9t - 4,9{t_0} + 19,6} \right) = - 9,8{t_0} + 19,6\)
Vậy hàm số \(h = 19,6t - 4,9{t^2}\) có đạo hàm là hàm số \(h' = - 9,8{t_0} + 19,6\)
Độ cao của vật khi nó chạm đất thỏa mãn \(19,6t - 4,9{t^2} = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 4\end{array} \right.\)
Khi t = 4, vận tốc của vật khi nó chạm đất là \( - 9,8.4 + 19,6 = - 19,6\) (m/s)
Vậy vận tốc của vật khi nó chạm đất là 19,6 m/s.

Ta có: \(v\left(t\right)=h'\left(t\right)=-9,8t\)
a, Vận tốc của vật tại thời điểm t = 5s là \(v\left(5\right)=-9,8\cdot5=-49\left(m/s\right)\)
b, Khi vật chạm đất thì \(h\left(t\right)=100-4,9t^2=0 \Rightarrow t=\dfrac{10\sqrt{10}}{7}\left(s\right)\)
Khi đó, vận tốc vật chạm đất là: \(v\left(\dfrac{10\sqrt{10}}{7}\right)=-9,8\cdot\dfrac{10\sqrt{10}}{7}=-14\sqrt{10}\left(m/s\right)\)

Để quả bóng ở độ cao trên 5m so với mặt đất thì:
\(\begin{array}{l}h(t) > 5\\ \Rightarrow - 4,9{t^2} + 20t + 1 > 5\\ \Rightarrow - 4,9{t^2} + 20t - 4 > 0\end{array}\)
Đặt \(f(t) = - 4,9{t^2} + 20t - 4\)có \(\Delta ' = b{'^2} - ac = {10^2} - ( - 4,9).( - 4) = 80,4 > 0\)nên \(f(t)\)có 2 nghiệm: \(\begin{array}{l}{t_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a} = \frac{{ - 10 + \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 - \sqrt {80,4} }}{{4,9}}\\{t_2} = \frac{{ - b' - \sqrt {\Delta '} }}{a} = \frac{{ - 10 - \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 + \sqrt {80,4} }}{{4,9}}\end{array}\)
Mặt khác \(a = - 4,9 < 0\), do đó ta có bảng xét dấu sau
Do đó để \(h(t) > 5\)thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\)
Vậy để quả bóng sẽ ở độ cao trên 5m so với mặt đất thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\)