Cho hàm số \(y = (x - 1)(2 - 3x)\)
a) Hàm số đã cho có phải hàm số bậc hai không? Nếu có, hãy xác định các hệ số a, b, c của nó.
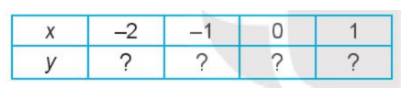
b) Thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá trị sau của hàm số đã cho.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)

Bài 2:
a: Thay x=1 và y=1 vào y=ax+5, ta được:
\(a\cdot1+5=1\)
=>a+5=1
=>a=-4
b: a=-4 nên y=-4x+5
| x | -2 | -1 | 0 | 1/2 | -3 |
| y=-4x+5 | 13 | 9 | 5 | 3 | -7 |
Bài 1:
a: \(y=-2\left(x+5\right)-4\)
\(=-2x-10-4\)
=-2x-14
a=-2; b=-14
b: \(y=\dfrac{1+x}{2}\)
=>\(y=\dfrac{1}{2}x+\dfrac{1}{2}\)
=>\(a=\dfrac{1}{2};b=\dfrac{1}{2}\)

Hàm số y = ax - 4 là hàm số bậc nhất nên a ≠ 0
a) Đồ thị hàm số y = ax – 4 cắt đường thẳng y = 2x – 1 tại điểm có hoành độ bằng 2 nên thay x = 2 vào phương trình hoành độ giao điểm ta có:
2a – 4 = 2.2 – 1 ⇔ 2a = 7 ⇔ a = 3,5
Kết hợp với điều kiện trên ta thấy a = 3,5 là giá trị cần tìm.
b) Đồ thị hàm số y = ax – 4 cắt đường thẳng y = -3x + 2 tại điểm A có tung độ bằng 5 nên đường thẳng y = -3x + 2 đi qua điểm có tung độ bằng 5. Thay tung độ vào phương trình đường thẳng ta được hoành độ của giao điểm A là:
5 = -3x + 2 ⇔ - 3x = 3 ⇔ x = -1
Ta được A(-1; 5).
Đường thẳng y = ax – 4 cũng đi qua điểm A(-1; 5) nên ta có:
5 = a.(-1) – 4 ⇔ -a = 9 ⇔ a = -9
Kết hợp với điều kiện trên ta thấy a = -9 là giá trị cần tìm.

Đồ thị hàm số y = ax – 4 cắt đường thẳng y = -3x + 2 tại điểm A có tung độ bằng 5 nên đường thẳng y = -3x + 2 đi qua điểm có tung độ bằng 5. Thay tung độ vào phương trình đường thẳng ta được hoành độ của giao điểm A là:
5 = -3x + 2 ⇔ - 3x = 3 ⇔ x = -1
Ta được A(-1; 5).
Đường thẳng y = ax – 4 cũng đi qua điểm A(-1; 5) nên ta có:
5 = a.(-1) – 4 ⇔ -a = 9 ⇔ a = -9
Kết hợp với điều kiện trên ta thấy a = -9 là giá trị cần tìm

a) Đồ thị của hàm số (1) cắt đường thẳng y = 2x - 1 tại điểm có hoành độ bằng 2 nên ta suy ra được :
x = 2 => y = 2.2 - 1 = 3
Thay y = 3 và x = 2 vào hàm số (1), ta được :
y = ax - 4
<=> 3 = a.2 - 4
<=> a.2 = 7
<=> a = 3,5
b) Đồ thị của hàm số (1) cắt đường thẳng y = -3x + 2 taiđiêrm có tung độ bằng 5 nên ta suy ra được :
y = 5
=> y = -3x + 2
<=> 5 = -3x + 2
<=> -3x = 3
<=> x = -1
Thay y = 5 và x = -1 vào hàm số (1), ta được :
y = ax - 4
<=> 5 = a.(-1) - 4
<=> a.(-1) = 9
<=> a = -9
bạn nhé.
a) Ta có \((x - 1)(2 - 3x) = 2x - 3{x^2} - 2 + 3x = - 3{x^2} + 5x - 2\)
Do đó hàm y=(x-1)(2-3x) là hàm số bậc hai với \(a = - 3;b = 5;c = - 2\)
b) Thay các giá trị của x vào y = (x - 1)(2 - 3x) ta có: