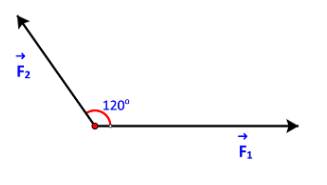
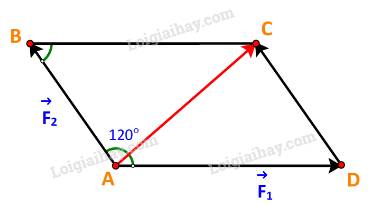
Bài 1 : Tính hợp lực của 2 lực đồng quy F1=16N , F2=12N trong các tường hợp góc hợp bởi hai lực lần lược là\(\alpha=0^o,\alpha=30^o,\alpha=60^o,\alpha=90^o,\alpha=120^o,\alpha=180^o\)Trong 4 trường hợp áp dụng\(F^2=F_1^2+F_1^2+2F_1F_2\cos\)\(\overrightarrow{F_1}\uparrow\uparrow\overrightarrow{F_2}\Rightarrow F=F_1+F_2\)\(\overrightarrow{F_1}\uparrow\downarrow\overrightarrow{F_2}\Rightarrow F=F_1-F_2\)\(\overrightarrow{F_1}L\overrightarrow{F_2}\Rightarrow...
Đọc tiếp
Bài 1 : Tính hợp lực của 2 lực đồng quy F1=16N , F2=12N trong các tường hợp góc hợp bởi hai lực lần lược là
\(\alpha=0^o,\alpha=30^o,\alpha=60^o,\alpha=90^o,\alpha=120^o,\alpha=180^o\)
Trong 4 trường hợp áp dụng
\(F^2=F_1^2+F_1^2+2F_1F_2\cos\)
\(\overrightarrow{F_1}\uparrow\uparrow\overrightarrow{F_2}\Rightarrow F=F_1+F_2\)
\(\overrightarrow{F_1}\uparrow\downarrow\overrightarrow{F_2}\Rightarrow F=F_1-F_2\)
\(\overrightarrow{F_1}L\overrightarrow{F_2}\Rightarrow F=\sqrt{F_1^2+F_2^2}\) chữ ''L'' là vuông góc nha
Bài 2: Một lò xo có chiều dài tự nhiên Lo=12cm khi bị kéo dãn lò xo dài 24cm và lực đàn hồi của nó là 5N .
Hỏi khi lực đàn hồi của lò xo là 10N thì chiều dài của lò xo = bao nhiêu ?
Công thức
\(F_2=K.\Delta l\)
\(=K\left|l-l_o\right|\)
\(F_2=K\left|l_{2_{ }}-lo\right|\)
Bài 3: Một vật trượt trên 1 sàn nằm ngang với vận tốc ban đầu vo=10m/s hệ số ma sát trượt là \(\mu=0,1\) . Hỏi
vật đi được quảng đường = bao nhiêu thì dừng lại cho g=10m/s2


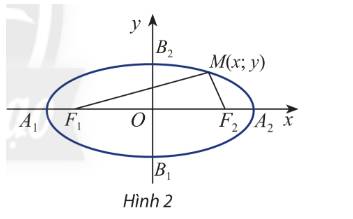
a) Phương trình tổng quát của đường thẳng \(A{F_1}{\rm{ }}\)là:\(\frac{x}{{ - 3}} + \frac{y}{4} = 1 \Leftrightarrow 4x - 3y + 12 = 0\).
Phương trình tổng quát của đường thẳng \(A{F_2}{\rm{ }}\)là:\(\frac{x}{3} + \frac{y}{4} = 1 \Leftrightarrow 4x + 3y - 12 = 0\).
b) Giả sử tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = I{F_1} = I{F_2} \Leftrightarrow I{A^2} = I{F_1}^2 = I{F_2}^2\)
Vì \(I{A^2} = I{F_1}^2,I{F_1}^2 = I{F_2}^2\) nên: \(\left\{ \begin{array}{l}{a^2} + {\left( {4 - b} \right)^2} = {\left( { - 3 - a} \right)^2} + {b^2}\\{\left( { - 3 - a} \right)^2} + {b^2} = {\left( {3 - a} \right)^2} + {b^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = \frac{7}{8}\end{array} \right.\) .
=> \(I\left( {0;\frac{7}{8}} \right)\) và \(R = IA = \sqrt {{0^2} + {{\left( {\frac{{25}}{8}} \right)}^2}} = \frac{{25}}{8}\)
Vậy phương trình đường tròn ngoại tiếp tam giác \(A{F_1}{F_2}\) là: \({x^2} + {\left( {y - \frac{7}{8}} \right)^2} = {\left( {\frac{{25}}{8}} \right)^2}\)
c) Gọi phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\).
Do elip có 2 tiêu điểm \({F_1},{F_2}\) nên \(\sqrt {{a^2} - {b^2}} = c = 3 \Leftrightarrow {a^2} - {b^2} = 9\).
Mặt khác điểm A thuộc elip nên \(\frac{{16}}{{{b^2}}} = 1 \Leftrightarrow b = 4\left( {do{\rm{ }}b > 0} \right)\). Vậy \(a = 5\).
Vậy phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{{5^2}}} + \frac{{{y^2}}}{{{4^2}}} = 1\).