Question

[Nguyễn Trần Thành Đạt]

Giá thuê xe ô tự lái là 1,2 triệu đồng một ngày cho hai ngày đầu tiên và 900 nghìn đồng cho mỗi ngày tiếp theo. Tổng số tiền T phải trả là một hàm số của số ngày x mà khách thuê xe. 

a) Viết công thức của hàm số T = T(x). 

b) Tính T(2), T(3), T(5) và cho biết ý nghĩa của mỗi giá trị này. 

Answer 1

[Hà Quang Minh]

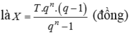
a)

Nếu \(0 < x \le 2\) thì \(T(x) = 1,2x\) (triệu đồng)

Nếu \(x > 2\) thì \(T(x) = 1,2.2 + 0,9.(x - 2) = 0,9x + 0,6\) (triệu đồng)

Số tiền phải trả sau khi thuê x ngày là

\(T(x) = \left\{ \begin{array}{l}1,2x\quad \quad \quad \;(0 < x \le 2)\\0,9x + 0,6\quad (x > 2)\end{array} \right.\)

b) \(T(2) = 1,2.2=2,4\)  (triệu đồng)

Ý nghĩa: số tiền khách phải trả khi thuê 2 ngày là 2,4 triệu đồng

\(T(3) = 0,9.3+0,6 = 3,3\)  (triệu đồng)

Ý nghĩa: số tiền khách phải trả khi thuê 3 ngày là 3,3 triệu đồng

\(T(5) = 0,9.5+0,6=5,1\)

Ý nghĩa: số tiền khách phải trả khi thuê 5 ngày là 5,1 triệu đồng