mn ơi cứu tôi với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
F
20 tháng 10 2021
1.khi có ánh sáng truyền vào mắt ta
2.khi có ánh sáng từ vật truyền vào mắt ta
3trong môi trường trong suốt và đồng tính ánh sáng truyền đi theo đường thẳng
tia phản xạ nằm trên cùng mặt phẳng với tia tới và pháp tuyến của gương
4,tia sáng đc biểu diễn bằng 1 đường thẳng có mũi tên chỉ lên trên
1 chùm sáng đc biểu diễn bằng cách vẽ hai tia sáng ngoài cùng của chùm sáng .
5,bóng tối là ko nhận đc ánh sáng
bóng nửa tối chỉ nhận đc 1 phần ánh sáng
hiện tượng nhật thực xảy ra khi TĐ,MT,Mặt Trăng cùng nằm trên 1 đường thẳng,mặt trăng nằm giữa TĐ và MT
hiện tượng nguyệt thực xảy ra khi TĐ,MT,Mặt Trăng nằm trên cùng 1 đường thẳng.TĐ nằm giữa MT và Mặt Trăng
6.Gương phẳng :ảnh ảo bằng vật
cầu lồi :nhỏ hơn vật
cầu lõm :lớn hơn vật
tick cho mình nhé
10 tháng 5 2022
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Xét ΔBDF và ΔEDC có
\(\widehat{BDF}=\widehat{EDC}\)
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
Do đó: ΔBDF=ΔEDC
MA
6 tháng 7 2023
2.
Đk: \(x>0,x\ne1\)
\(B=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x-1}\right)}+\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{2-x}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-\sqrt{x}+\sqrt{x}-1+\sqrt{x}+2-x}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
Vậy B=...
3.\(A=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}\) , \(\dfrac{A}{B}=\dfrac{x}{\sqrt{x}-1}\)
\(P< 0\Leftrightarrow\dfrac{x}{\sqrt{x}-1}< 0\) \(\Leftrightarrow\sqrt{x}-1< 0\left(dox>0\right)\)
\(\sqrt{x}< 1\Leftrightarrow0< x< 1\)
Vậy \(0< x< 1\) thì P âm.
mn ơi cứu minh với
13 tháng 7 2023
\(A=\dfrac{1}{4}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}\right)\)
=>\(A< \dfrac{1}{4}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\right)\)
=>A<1/4*1=1/4
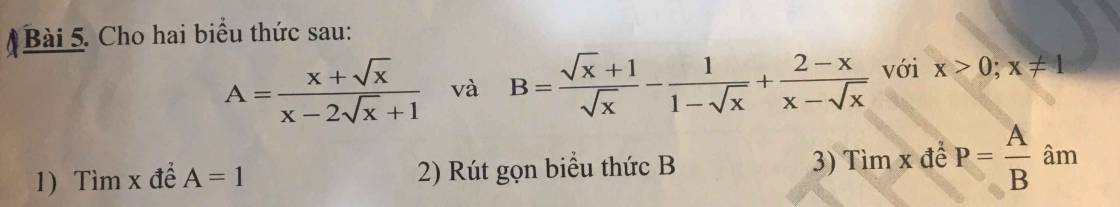
⇒ AH cũng là đường trung tuyến của ∆ABC
⇒ H là trung điểm của BC
Lại có HD = HA (gt)
⇒ H là trung điểm của AD
Ta có:
AH ⊥ BC
⇒ AD ⊥ BC
Xét tứ giác ABDC có:
H là trung điểm của BC (cmt)
H là trung điểm của AD (cmt)
⇒ ABDC là hình bình hành
Mà AD ⊥ BC (cmt)
⇒ ABDC là hình thoi
b) Do H là trung điểm của BC (cmt)
⇒ BH = BC : 2 = 6 : 2 = 3 (cm)
∆ABH vuông tại H (do AH ⊥ BC)
⇒ AB² = AH² + BH² (Pytago)
⇒ AH² = AB² - BH²
= 5² - 3²
= 16
⇒ AH = 4 (cm)
⇒ AD = AH = 4 (cm)
c) Tứ giác AHCF có:
E là trung điểm AC (gt)
E là trung điểm FH (gt)
⇒ AHCF là hình bình hành
Mà ∠AHC = 90⁰ (AH ⊥ BC)
⇒ AHCF là hình chữ nhật
⇒ AF ⊥ AH và FC ⊥ CH
d) Do ABDC là hình thoi (cmt)
⇒ ∠BAC = ∠BDC = 60⁰
Ta có:
∠BAC + ∠BDC + ∠ABD + ∠ACD = 360⁰ (tổng các góc của hình thoi ABDC)
⇒ ∠ABD + ∠ACD = 360⁰ - (∠BAC + ∠BDC)
= 360⁰ - (60⁰ + 60⁰)
= 360⁰ - 120⁰
= 240⁰
Mà ∠ABD = ∠ACD (hai góc đối của hình thoi ABDC)
⇒ ∠ABD = ∠ACD = 240⁰ : 2 = 120⁰
Vậy các góc của hình thoi ABDC lần lượt là:
∠BAC = ∠BDC = 60⁰
∠ABD = ∠ACD = 120⁰