Cho mệnh đề Q: “Châu Á là châu lục có diện tích lớn nhất trên thế giới”. Phát biểu mệnh đề phủ định \(\overline Q \) và xác định tính đúng sai của hai mệnh đề Q và \(\overline Q \).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Mệnh đề phủ định của mệnh đề P là \(\overline P \): “2 022 không chia hết cho 5”
Mệnh đề \(\overline P \) đúng.
Mệnh đề phủ định của mệnh đề Q là \(\overline Q \): “Bất phương trình \(2x + 1 > 0\) vô nghiệm”.
Mệnh đề \(\overline Q \) sai vì bất phương trình \(2x + 1 > 0\) có nghiệm, chẳng hạn: \(x = 0;\;x = 1\).
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
+) Mệnh đề \(P \Rightarrow Q\) là: “Vì tam giác ABC đều nên tam giác ABC cân và có một góc bằng \({60^o}\)”.
+) Mệnh đề \(Q \Rightarrow P\) là: “Tam giác ABC cân và có một góc bằng \({60^o}\) suy ra tam giác ABC đều”.
Dễ thấy cả hai mệnh đề trên đều đúng.
+) Mệnh đề tương đương: (dùng một trong các cách sau:)
“Tam giác ABC đều tương đương tam giác ABC cân và có một góc bằng \({60^o}\)”
“Tam giác ABC đều là điều kiện cần và đủ để có tam giác ABC cân và có một góc bằng \({60^o}\)”
“Tam giác ABC đều khi và chỉ khi tam giác ABC cân và có một góc bằng \({60^o}\)”
“Tam giác ABC đều nếu và chỉ nếu tam giác ABC cân và có một góc bằng \({60^o}\)”
CM
15 tháng 1 2018
Mệnh đề phủ định của P: P− “ π không là một số hữu tỉ”.
P là mệnh đề sai, P− là mệnh đề đúng.
Mệnh đề phủ định của Q: Q− “Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh thứ ba”.
Q là mệnh đề đúng, Q− là mệnh đề sai.
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) Mệnh đề \(P \Rightarrow Q\) là: “Nếu \({a^2} < {b^2}\) thì \(0 < a < b\)”
b) Mệnh đề \(Q \Rightarrow P\) là: “Nếu \(0 < a < b\) thì \({a^2} < {b^2}\)”
c) Mệnh đề \(P \Rightarrow Q\) là: “Nếu \({a^2} < {b^2}\) thì \(0 < a < b\)” sai,
Chẳng hạn \(a = 2;\;b = -3\) ta có: \({2^2} < {( - 3)^2}\) nhưng không suy ra \(0<2<-3\).
Mệnh đề \(Q \Rightarrow P\) là: “Nếu \(0 < a < b\) thì \({a^2} < {b^2}\)” đúng.
HJ
Xác định tính đúng sai của mệnh đề sau và tìm mệnh đề phủ định của nó:
Q:"∃nϵN,n chia hết cho n + 1"
1
5 tháng 7 2023
Mệnh đề này đúng
Vì với n=0 thì 0 chia hết cho 0+1
Mệnh đề phủ định: \(\overline{Q}\forall n\in N;n⋮̸n+1\)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
P: “tam giác ABC vuông tại A”
Q: “tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)”
+) Mệnh đề \(Q \Rightarrow P\) là “Nếu tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)thì tam giác ABC vuông tại A”
+) Từ định lí Pytago, ta có:
Tam giác ABC vuông tại A thì \(A{B^2} + A{C^2} = B{C^2}\)
Và: Tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\) thì vuông tại A.
Do vậy, hai mệnh đề “\(P \Rightarrow Q\)” và “\(Q \Rightarrow P\)” đều đúng.
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
+) Mệnh đề phủ định của mệnh đề P là \(\overline P \): “5,15 không phải là một số hữu tỉ”
Mệnh đề P đúng, \(\overline P \) sai vì \(5,15 = \frac{{103}}{{20}} \in \mathbb{Q}\), là một số hữu tỉ.
+) Mệnh đề phủ định của mệnh đề Q là \(\overline Q \): “2 023 không phải là số chẵn” (hoặc “2 023 là số lẻ”)
Mệnh đề Q sai, \(\overline Q \) đúng vì 2 023 có chữ số tận cùng là \(3 \ne \left\{ {0;2;4;6;8} \right\}\), đo đó 2 023 không phải là số chẵn.
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
23 tháng 9 2023
P: đúng
phủ định: "5,15 không phải số hữu tỉ"
Q: sai
Phủ định: "1023 không phải số chẵn"
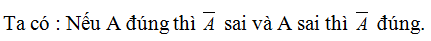
Mệnh đề phủ định của Q là \(\overline Q \): “Châu Á không phải là châu lục có diện tích lớn nhất trên thế giới”.
Châu Á phần lớn nằm ở Bắc bán cầu, là châu lục có diện tích lớn nhất trên thế giới.
Do đó Q là mệnh đề đúng, \(\overline Q \) là mệnh đề sai.