Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(C'\left(x\right)=\left(\sqrt{5x^2+60}\right)'=\dfrac{\left(5x^2+60\right)'}{2\sqrt{5x^2+60}}\)
\(=\dfrac{10x}{2\sqrt{5x^2+60}}=\dfrac{5x}{\sqrt{5x^2+60}}\)
\(x'\left(t\right)=20\)
\(C'\left(t\right)=C'\left(x\right)\cdot x'\left(t\right)=\dfrac{100\left(2t+40\right)}{\sqrt{5\left(20t+40\right)^2+60}}\)
\(C'\left(4\right)=\dfrac{100\left(2\cdot4+40\right)}{\sqrt{5\left(80+40\right)^2+60}}\simeq44,7\)
a, Hàm chi phí biên là:
\(C'\left(Q\right)=2Q+80\)
b, \(C'\left(90\right)=2\cdot90+80=260\left(USD\right)\)
Ý nghĩa: Chi phí gia tăng để sản xuất thêm 1 sản phẩm từ 89 sản phẩm lên 90 sản phẩm là 260 (USD)
c, Chi phí sản xuất máy vô tuyến thứ 100 là:
\(C'\left(100\right)=2\cdot100+80=280\left(USD\right)\)
Doanh thu khi bán Q sản phẩm là 170Q nghìn đồng.
Lợi nhuận khi bán Q sản phẩm là \(170Q - \left( {{Q^2} + 30Q + 3300} \right)\)\( = - {Q^2} + 140Q - 3300\)(nghìn đồng)
Để không bị lỗ thì \( - {Q^2} + 140Q - 3300 \ge 0\left( 1 \right)\)
\(a = - 1 < 0;\Delta ' = 1600\)
\( - {Q^2} + 140Q - 3300 = 0\) có 2 nghiệm phân biệt \({x_1} = 30,{x_2} = 110\)
(1)\( \Leftrightarrow \)\(30 \le x \le 110\)
Vậy để không bị lỗ thì số sản phẩm được sản suất phải nằm trong khoảng từ 30 đến 110 sản phẩm.
Ta có x ∈ (0; 60000)
Do đó, hàm số đạt cực tiểu tại x = 50000.
Nên x=50000 là số sản phẩm cần sản xuất mỗi ngày để tối thiểu chi phí.
Chọn C
Chọn A.
Gọi x; y lần lượt là số phẩm loại A; B.
Theo đề bài ta có: 2000x + 4000y = 40 000 hay x + 2y = 20
Suy ra: x = 20 - 2y.
Ta có 
Xét hàm 
Tập xác định D = (0; 10).
Nhận xét: 
nên dấu của y’ là dấu của biểu thức 
Do đó hàm số đạt giá trị lớn nhất khi y = 6 và x = 8
Vậy 
Ta có C ' x = 2 x 2 - 24 x + 70 x - 6 2
C ' x = 0 ⇔ x = 5 x = 7 So điều kiện x > 6, chọn x = 7
Vậy để tổng chi phí lớn nhất thì công ty cần cải tiến 7 đơn vị sản phẩm
Đáp án D
Đáp án B
Thể tích của mỗi thỏi son hình trụ là:
V = π r 2 h = 20 , 25 π ⇔ r 2 h = 20 , 25 ⇔ h = 20 , 25 r 2
Ta có:
T = 60000 r 2 + 20000 r h = 60000 r 2 + 20000 r . 20 , 25 r 2 = 60000 r 2 + 405000 r
60000 r 2 + 202500 r + 202500 r ≥ 3 60000 r 2 . 202500 r . 202500 r 3 = 405000
Dấu “=” xảy ra khi:
60000 r 2 = 202500 r ⇔ r = 3 2 ⇒ h = 9 ⇒ r + h = 10 , 5 c m
Theo đề bài, giá bán \(x\) sản phẩm là \(170x\) (nghìn đồng)
Để nhà sản xuất không bị lỗ thì \(P\left(x\right)\le170x\) \(\Leftrightarrow x^2+30x+3300\le170x\) \(\Leftrightarrow x^2-140x+3300\le0\) \(\Leftrightarrow\left(x-110\right)\left(x-30\right)\le0\)
Đặt \(f\left(x\right)=\left(x-110\right)\left(x-30\right)\). Ta lập bảng xét dấu:
| \(x\) | \(-\infty\) \(30\) \(110\) \(+\infty\) |
| \(f\left(x\right)\) | \(+\) \(0\) \(-\) \(0\) \(+\) |
Vậy \(f\left(x\right)\le0\Leftrightarrow x\in\left[30;110\right]\). Do đó, để nhà sản xuất không bị lỗ thì số sản phẩm được sản xuất trong đoạn \(\left[30;110\right]\).
Giá của x sản phẩn là:
x ( 120 -x ) = - x2 +120x
Lợi nhuận còn lại:
\(-x^2+120x-C\left(x\right)=-x^2+120x-x^2-5x-300=-2x^2+115x-300\)
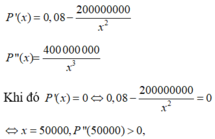
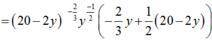
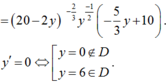
a) \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{50000 + 105x}}{x}\)
b) \(\mathop {\lim }\limits_{x \to + \infty } \overline C \left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{50000 + 105x}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {\frac{{50000}}{x} + 105} \right)}}{x} = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{50000}}{x} + 105} \right) = 0 + 105 = 105\)
Vậy khi số sản phẩm càng lớn thì chi phí trung bình để sản xuất một sản phẩm tối đa 105 (nghìn đồng).