Ông An vay ngân hàng 1 tỉ đồng, với lãi suất 12%/năm. Ông đã trả nợ theo cách: Bắt đầu từ tháng thứ nhất sau khi vay, cuối mỗi tháng ông trả ngân hàng cùng số tiền là a (đồng) và đã trả hết nợ sau đúng 2 năm kể từ ngày vay. Hỏi số tiền mỗi tháng mà ông An phải trả là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Vay vốn trả góp: Vay ngân hàng số tiền là P đồng với lãi suất r% trên tháng. Sau đúng một tháng kể từ ngày vay, bắt đầu hoàn nợ; hai lần hoàn nợ cách nhau đúng một tháng, mỗi tháng hoàn nợ số tiền là X đồng và trả hết số tiền nợ sau đúng n tháng



Đáp án B
Áp dụng CT trả góp ta có m = 100 1 + 12 % 12 12 12 % 12 1 + 12 % 12 12 − 1 ≈ 0 , 885 triệu đồng

Đây là câu 21 của đề minh họa thị THPT QG 2017.
Lãi suất 12%/năm => lãi suất 1%/tháng.
Nếu còn nợ a đồng thì phải trả lãi 0,01 a cho 1 tháng.
Sau tháng đầu tiên, sau khi trả m đồng thì ông A còn nợ là:
(a + 0,01.a) - m = a. 1,01 - m
Sau tháng thứ hai, sau khi trả tiếp m đồng thì ông A còn nợ là:
(a . 1,01 - m) . 1,01 - m
Sau tháng thứ ba, sau khi trả tiếp m đồng thì ông A còn nợ là:
[(a. 1,01 - m) . 1,01 - m] . 1,01 - m
Con số nợ cuối cùng này phải bằng 0, suy ra:
[(a. 1,01 - m) . 1,01 - m] . 1,01 - m = 0
=> \(m=\frac{a.1,01^3}{1,01^2+1,01+1}=\frac{a.1,01^3\left(1,01-1\right)}{1,01^3-1}=\frac{a.1,01^3.0,01}{1,01^3-1}\)
Thay a = 100 vào ta có:
\(m=\frac{1,01^3}{1,01^3-1}\)


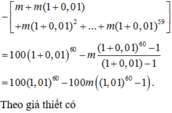
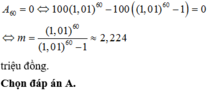
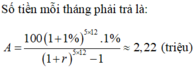
Gọi unn là số tiền sau mỗi tháng ông An còn nợ ngân hàng.
Lãi suất mỗi tháng là 1% .
Ta có:
u1 = 1 000 000 000 đồng.
u2 = u1 + u1.1% - a = u1(1 + 1%) – a (đồng)
u3 = u1(1 + 1%) – a + [u1(1 + 1%) – a].1% – a = u1(1 + 1%)2 – a(1 + 1%) – a
...
un = u1(1 + 1%)n-1 – a(1 + 1%)n-2 – a(1 + 1%)n-3 – a(1 + 1%)n-4 – ... – a.
Ta thấy dãy a(1 + 1%)n-1; a(1 + 1%)n-3; a(1 + 1%)n-4; ...; a lập thành một cấp số nhân với số hạng đầu a1 = a và công bội q = 1 + 1% = 99% có tổng n – 2 số hạng đầu là:
\({S_{n - 2}} = \frac{{a\left[ {1 - {{\left( {99\% } \right)}^{n - 2}}} \right]}}{{1 - 99\% }} = 100a\left[ {1 - {{\left( {99\% } \right)}^{n - 2}}} \right]\).
Suy ra un = u1(1 + 1%)n-1 – 100a[1 – (99%)n-2].
Vì sau 2 năm = 24 tháng thì ông An trả xong số tiền nên n = 24 và u24 = 0. Do đó ta có:
u24 = u1(1 + 1%)23 – 100a[1 – (99%)22] = 0
⇔ 1 000 000 000.(99%) – 100a[1 – (99%)22] = 0
⇔ a = 40 006 888,25
Vậy mỗi tháng ông An phải trả 40 006 888,25 đồng.