Question

[Quoc Tran Anh Le]

Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (m) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày \(\left( {0 \le t < 24} \right)\) cho bởi công thức \(h = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\). Tìm t để độ sâu của mực nước là

a)     15m

b)     9m

c)     10,5m

Answer 1

[Hà Quang Minh]

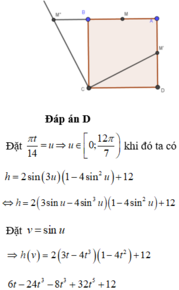
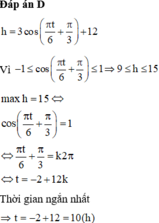
+) Độ sâu của mực nước là 15m thì h = 15.

Khi đó

 \(\begin{array}{l}15 = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = 1\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = \cos 0\\ \Leftrightarrow \frac{{\pi t}}{6} + 1 = k2\pi \\ \Leftrightarrow t = \frac{{6\left( {k2\pi  - 1} \right)}}{\pi };k \in Z\end{array}\)

Vì \(0 \le t < 24\) nên

 \(\begin{array}{l}0 \le \frac{{6\left( {k2\pi  - 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 < k \le 2\end{array}\)

Lại do \(k \in Z \Rightarrow k \in \left\{ {1;2} \right\} \Rightarrow t \in \left\{ {\frac{{6\left( {2\pi  - 1} \right)}}{\pi };\frac{{6\left( {4\pi  - 1} \right)}}{\pi }} \right\}\)

+) Độ sâu của mực nước là 9m thì h = 9.

Khi đó

 \(\begin{array}{l}9 = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) =  - 1\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = \cos \pi \\ \Leftrightarrow \frac{{\pi t}}{6} + 1 = \pi  + k2\pi \\ \Leftrightarrow t = \frac{{6\left( {k2\pi  + \pi  - 1} \right)}}{\pi };k \in Z\end{array}\)

Vì \(0 \le t < 24\) nên

 \(\begin{array}{l}0 \le \frac{{6\left( {k2\pi  + \pi  - 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 < k \le 1\end{array}\)

Lại do \(k \in Z \Rightarrow k = 1 \Rightarrow t = \frac{{6\left( {3\pi  - 1} \right)}}{\pi }\)

+) Độ sâu của mực nước là 10,5m thì h = 10,5.

Khi đó

 \(\begin{array}{l}10,5 = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) =  - \frac{1}{2}\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = \cos \frac{{2\pi }}{3}\\ \Leftrightarrow \left[ \begin{array}{l}\frac{{\pi t}}{6} + 1 = \frac{{2\pi }}{3} + k2\pi \\\frac{{\pi t}}{6} + 1 =  - \frac{{2\pi }}{3} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{6\left( {\frac{{2\pi }}{3} + k2\pi  - 1} \right)}}{\pi };k \in Z\\t = \frac{{6\left( { - \frac{{2\pi }}{3} + k2\pi  - 1} \right)}}{\pi };k \in Z\end{array} \right.\end{array}\)

Với \(t = \frac{{6\left( {\frac{{2\pi }}{3} + k2\pi  - 1} \right)}}{\pi };k \in Z\)

Vì \(0 \le t < 24\) nên

 \(\begin{array}{l}0 \le \frac{{6\left( {\frac{{2\pi }}{3} + k2\pi  - 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 \le k \le 2\end{array}\)

Lại do \(k \in Z \Rightarrow k \in \left\{ {0;1;2} \right\} \Rightarrow t \in \left\{ {\frac{{6\left( {\frac{{2\pi }}{3} - 1} \right)}}{\pi };\frac{{6\left( {\frac{{8\pi }}{3} - 1} \right)}}{\pi };\frac{{6\left( {\frac{{14\pi }}{3} - 1} \right)}}{\pi }} \right\}\)

Với \(t = \frac{{6\left( { - \frac{{2\pi }}{3} + k2\pi  - 1} \right)}}{\pi };k \in Z\)

Vì \(0 \le t < 24\) nên

 \(\begin{array}{l}0 \le \frac{{6\left( { - \frac{{2\pi }}{3} + k2\pi  - 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 < k \le 2\end{array}\)

Lại do \(k \in Z \Rightarrow k \in \left\{ {1;2} \right\} \Rightarrow t \in \left\{ {\frac{{6\left( { - \frac{{2\pi }}{3} - 1} \right)}}{\pi };\frac{{6\left( {\frac{{4\pi }}{3} - 1} \right)}}{\pi };\frac{{6\left( {\frac{{10\pi }}{3} - 1} \right)}}{\pi }} \right\}\)