Hãy nhắc lại cách nhân hai đơn thức và tính (12x3).(-5x2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
Khoảng cách hai điểm M,I (hay độ dài đoạn thẳng MI) chính là độ dài vecto \(\overrightarrow {MI} \)
\(\overrightarrow {MI} = \left( {a - x;b - y} \right) \Rightarrow \left| {\overrightarrow {MI} } \right| = \sqrt {{{\left( {a - x} \right)}^2} + {{\left( {;b - y} \right)}^2}} \)
Vậy khoảng cách giữa hai điểm \(I\left( {a;b} \right)\) và \(M\left( {x;y} \right)\) là \(\sqrt {{{\left( {a - x} \right)}^2} + {{\left( {;b - y} \right)}^2}} \)
ND
2
11 tháng 9 2021
\(8x\left(x-2\right)-3\left(x^2-4x-5\right)-5x^2\)
\(=8x^2-16x-3x^2+12x+15-5x^2\)
\(=15-4x\)
12 tháng 9 2021
`8x(x-2) -3 (x^2 -4x-5)-5x^2`
`= 8x^2 - 16x - 3x^2 +12x+15 - 5x^2`
`= (8x^2 - 3x^2 - 5x^2)+(-16x +12x)+15`
`= -4x +15`
CM
12 tháng 1 2017
a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích:
QT
1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) 12x3 : 4x = (12:4) . (x3 : x) = 3.x2
b) (-2x4 ) : x4 = [(-2) : 1] . (x4 : x4) = -2
c) 2x5 : 5x2 = (2:5) . (x5 : x2) = \(\frac{2}{5}\)x3
CM
20 tháng 10 2018
Ta có:
A(x) + B(x) = -2x3 + 9 - 6x + 7x4 - 2x2+ 5x2 + 9x - 3x4 + 7x3 - 12
= 4x4 + 5x3 + 3x2 + 3x - 3. Chọn B
PT
1
CM
1 tháng 9 2017
Công thức tính thể tích lăng trụ có diện tích đáy là B và chiều cao là h là: V = B*h
PT
30 tháng 3 2017
Định lí:
Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.
Ta có các hệ thức sau: a2 = b2 + c2 - 2bc.cosA (1)
b2 = a2 + c2 - 2bc.cosB (2)
c2 = a2 + b2 - 2bc.cosC (3)
Hệ quả: Từ định lí cosin suy ra:
cosA = cosB =
cosC =
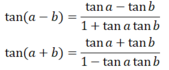
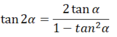
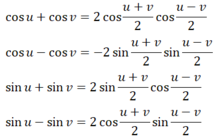
+ Cách nhân 2 đơn thức: Muốn nhân 2 đơn thức, ta nhân hai hệ số với nhau và nhân hai lũy thừa của biến với nhau.
+ Ta có:
(12x3).(-5x2) = 12. (-5). (x3 . x2) = -60 . x5