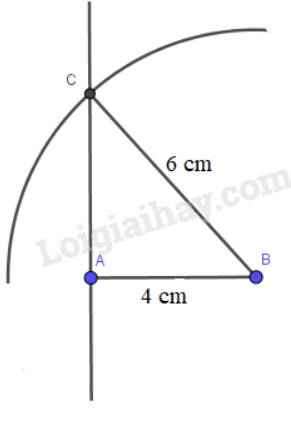
Vẽ tam giác ABC vuông tại A có AB = 4 cm, BC = 6 cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
KS
Kiều Sơn Tùng
18 tháng 9 2023
Đúng(0)
Những câu hỏi liên quan
5 tháng 2 2022
a: BC=10cm
C=AB+BC+AC=6+8+10=24(cm)
b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
c: Ta có: ΔABD=ΔHBD
nên DA=DH
mà DH<DC
nên DA<DC
3 tháng 2 2022
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có \(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
2: Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3.6\left(cm\right)\)
3: Xét ΔBAC có BK là đường phân giác
nên \(\dfrac{AK}{KC}=\dfrac{AB}{BC}\)
mà \(\dfrac{AB}{BC}=\dfrac{BH}{AB}\)
nên \(\dfrac{AK}{KC}=\dfrac{BH}{AB}\left(1\right)\)
Xét ΔAHC vuông tại H và ΔBHA vuông tại H có
\(\widehat{HAC}=\widehat{HBA}\)
Do đó: ΔAHC\(\sim\)ΔBHA
Suy ra: \(\dfrac{AC}{AB}=\dfrac{AH}{BH}\)
=>BH/AH=AB/AC
hay \(\dfrac{BH}{AB}=\dfrac{AH}{AC}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AK}{KC}=\dfrac{AH}{AC}\)
hay \(AK\cdot AC=AH\cdot KC\)
12 tháng 2 2022
Bài 4 :
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=35cm\)
Bài 5 :
Theo định lí Pytago tam giác MNO vuông tại O
\(OM=\sqrt{MN^2-ON^2}=33cm\)
12 tháng 2 2022
Bài 4:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{21^2+28^2}=35\left(cm\right)\)
Bài 5:
\(OM=\sqrt{55^2-44^2}=33\left(cm\right)\)
MH
12 tháng 5 2022
(Tự vẽ hình)
a) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
b) Xét \(\Delta ABD\) và \(\Delta HBD\) có:
\(\widehat{BAD}=\widehat{BHD}=90^0\)
\(BD\) chung
\(\widehat{ABD}=\widehat{HBD}\) (tính chất phân giác)
\(\Rightarrow\Delta ABD=\Delta HBD\) (ch - gn)
c) Ta có \(\Delta ABD=\Delta HBD\Rightarrow AD=HD\)
Mà \(HD< DC\) (do \(\Delta HDC\) vuông tại \(H\))
\(\Rightarrow DA< DC\)
12 tháng 5 2022
a, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AC^2+AB^2}=10cm\)
b, Xét tam giác BAD và tam giác BHD có
BD _ chung ; ^ABD = ^HBD ; ^BAD = ^BHD = 900
Vậy tam giác BAD = tam giác BHD ( ch-gn)
19 tháng 3 2022
a, Xét tg AHB và tg AHC, có:
AB=AC(tg cân)
góc AHB= góc AHC(=90o)
góc B= góc C(tg cân)
=> tg AHB= tg AHC(ch-gn)
b,Xét tg BMH và tg CNH, có:
góc B= góc C(tg cân)
BH=CH(2 cạnh tương ứng)
góc BMH= góc CNH(=90o)
=> tg BMH= tg CNH(ch-gn)
Xét tg AMH và tg ANH, có:
AH chung.
góc AMH= góc ANH(=90o)
MH=HN(2 cạnh tương ứng)
=> tg AMH= tg ANH(ch- cgv)
=> AM=AN(2 cạnh tương ứng)
=> tg AMN là tg cân.
c, Ta có:tg AMN cân tại A, tg ABC cân tại A nên, suy ra:
Các góc ở đáy bằng nhau: góc B= góc C= góc AMN= góc ANM.
Mà góc AMN và góc B ở vị trí đồng vị nên, suy ra:
MN // BC.
HBA
BC). Tính BD, CD.
13 tháng 5 2022
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
Do đó: ΔHBA\(\sim\)ΔABC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=4.8\left(cm\right)\)