1 vật dao động điều hòa với biên độ A = 4cm và tần số 5Hz khi vật có li độ x = 2cm thì tốc độ và gia tốc của vật dao động là bao nhiêu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử pt dao động của vật có dạng:
\(x=Acos\left(5t+\varphi\right)\left(cm\right)\)
\(\Rightarrow v=-5Asin\left(5t+\varphi\right)=5Acos\left(\dfrac{\pi}{2}+5t+\varphi\right)\left(\text{cm/s}\right)\)
Tại \(t=0:\)\(\left\{{}\begin{matrix}x=-2\left(cm\right)\\v=10\left(\text{cm/s}\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=Acos\varphi=-2\left(cm\right)\\v_0=5Acos\left(\dfrac{\pi}{2}+\varphi\right)=10\left(\text{cm/s}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=-\dfrac{2}{A}\left(1\right)\\5A\left(cos\dfrac{\pi}{2}.cos\varphi-sin\dfrac{\pi}{2}.sin\varphi\right)=10\end{matrix}\right.\)
\(\Rightarrow5A.\left(-sin\varphi\right)=10\Leftrightarrow sin\varphi=\dfrac{-2}{A}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\varphi=\dfrac{-3\pi}{4}\left(rad\right);A=2\sqrt{2}\left(cm\right)\)
Vậy ta có ptdđ của vật: \(x=2\sqrt{2}cos\left(5t-\dfrac{3\pi}{4}\right)\left(cm\right)\)
b)\(v_{max}=\omega A=5A=10\sqrt{2}\left(\text{cm/s}\right)\)
\(a_{max}=\omega^2A=50\sqrt{2}\left(\text{cm/s}^2\right)\)
c) \(\alpha=\Delta t.\omega=1,4\pi.5=7\pi\left(rad\right)=6\pi+\pi\left(rad\right)\)
\(\Rightarrow S=3.4A+2\sqrt{2}-2+2\sqrt{2}+2=12A+4\sqrt{2}=28\sqrt{2}\left(cm\right)\)

ü Đáp án B
v ω A 2 + a ω 2 A 2 = 1 ⇒ ω = 4 rad/s.
+ Áp dụng hệ thức độc lập giữa vận tốc và gia tốc:

Đáp án B
Áp dụng hệ thức độc lập giữa vận tốc
và gia tốc v ω A 2 + a ω 2 A 2 = 1 ⇒ ω = 4 r a d / s

+ Áp dụng hệ thức độc lập giữa vận tốc và gia tốc:
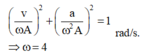
Đáp án B

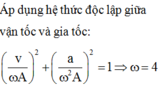
\(f=5Hz=>\omega=\dfrac{2\pi}{f}=\dfrac{2\pi}{5} \\ A^2=x^2+\dfrac{v^2}{\omega^2}\\ < =>v^2=\omega^2\left(A^2-x^2\right)\\ < =>v^2=\dfrac{2\pi}{5}\left(4^2-2^2\right)\\ < =>v^2=\dfrac{24\pi}{5}\\ < =>v=\dfrac{2\sqrt{6}\pi}{5}\)
\(a=A\omega^2\\ < =>a=4.\left(\dfrac{2\pi}{5}\right)^2\\ < =>a=\dfrac{16\pi}{25}\)