Một vật chuyển động đều trên một quãng đường dài 254km. Viết đẳng thức tìm vận tốc v (km/h) theo thời gian t (h).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
Với t = 3 thì v = \(\frac{{240}}{3} = 80\)
Với t = 4 thì v = \(\frac{{240}}{4} = 60\)
Với t = 5 thì v = \(\frac{{240}}{5} = 48\)
Với t = 6 thì v = \(\frac{{240}}{6} = 40\)
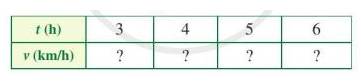
t (h) | 3 | 4 | 5 | 6 |
v (km/h) | 80 | 60 | 48 | 40 |
KV
3 tháng 12 2023
a) Gọi t (h) là thời gian chuyển động của vật
Khi đó, s = 20t
b) c = 4a
3 tháng 12 2023
a) Quãng đường �s (kilômét) đi được theo thời gian �t (giờ) của một vật chuyển động đều với vận tốc �v (kilômét/giờ) có thể được tính bằng công thức:
�=�×�s=v×t
Trong trường hợp này, nếu vận tốc �v là 20 km/h và thời gian �t là số giờ di chuyển, thì công thức tính quãng đường đi được sẽ là:
�=20×�s=20×t
b) Chu vi �c (centimét) của một hình vuông có thể được tính từ cạnh có độ dài �a (centimét). Vì hình vuông có bốn cạnh bằng nhau, chu vi của hình vuông sẽ bằng tổng độ dài các cạnh, tức là:
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
Công thức tính quãng đường là :
S = v.t
Theo đề bài S = 200km nên ta có 200 = v.t
Vì v.t = 200 không đổi nên v tỉ lệ nghịch với t theo hệ số tỉ lệ là 200.
\( \Rightarrow t=\dfrac{{200}}{v}\)
4 tháng 1 2022
Gọi quãng đường xe đi trong nửa thời gian đầu và nửa thời gian sau là \(M_1;M_2\)
Quãng đường xe đi trong nủa thời gian đầu là: \(M_1=v_1.\frac{1}{2}t=10t\)
Quãng đường xe đi trong nủa thời gian sau là: \(M_2=v_2.\frac{1}{2}t=15\)
Vận tốc trung bình của xe là: \(v_{tb}=\frac{M_1+M_2}{t}=\frac{10t+15t}{t}=\frac{25}{t}=25km/h\)
1 tháng 11 2021
bài 1:
tóm tắt
\(s=18km=18000m\)
\(t=30'=1800s\)\(=0,5h\)
\(v=?\)
giải
ADCT: \(v=\dfrac{s}{t}\); ta có:
vận tốc của ô tô theo đơn vị km/h là:
\(\dfrac{18}{0,5}=36\left(km/h\right)\)
vận tốc của ô tô theo đơn vị m/s là:
\(\dfrac{18000}{1800}=10\left(m/s\right)\)
1 tháng 11 2021
bài 2:
tóm tắt
\(s=9000m=9km\)
\(v=45km/h\)
\(t=?\)
giải:
ADCT: \(v=\dfrac{s}{t}\Rightarrow t=\dfrac{s}{v}\); ta có:
thời gian mà xe máy di chuyển hết quãng đường AB là:
\(\dfrac{9}{45}=\dfrac{1}{5}=0,2\left(h\right)\)
\(v=\frac{254}{t}\)[km/h]
AI THẤY ĐÚNG THÌ ỦNG HỘ NHA