Bài mik để dưới phần trả lời ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
4 tháng 7 2023
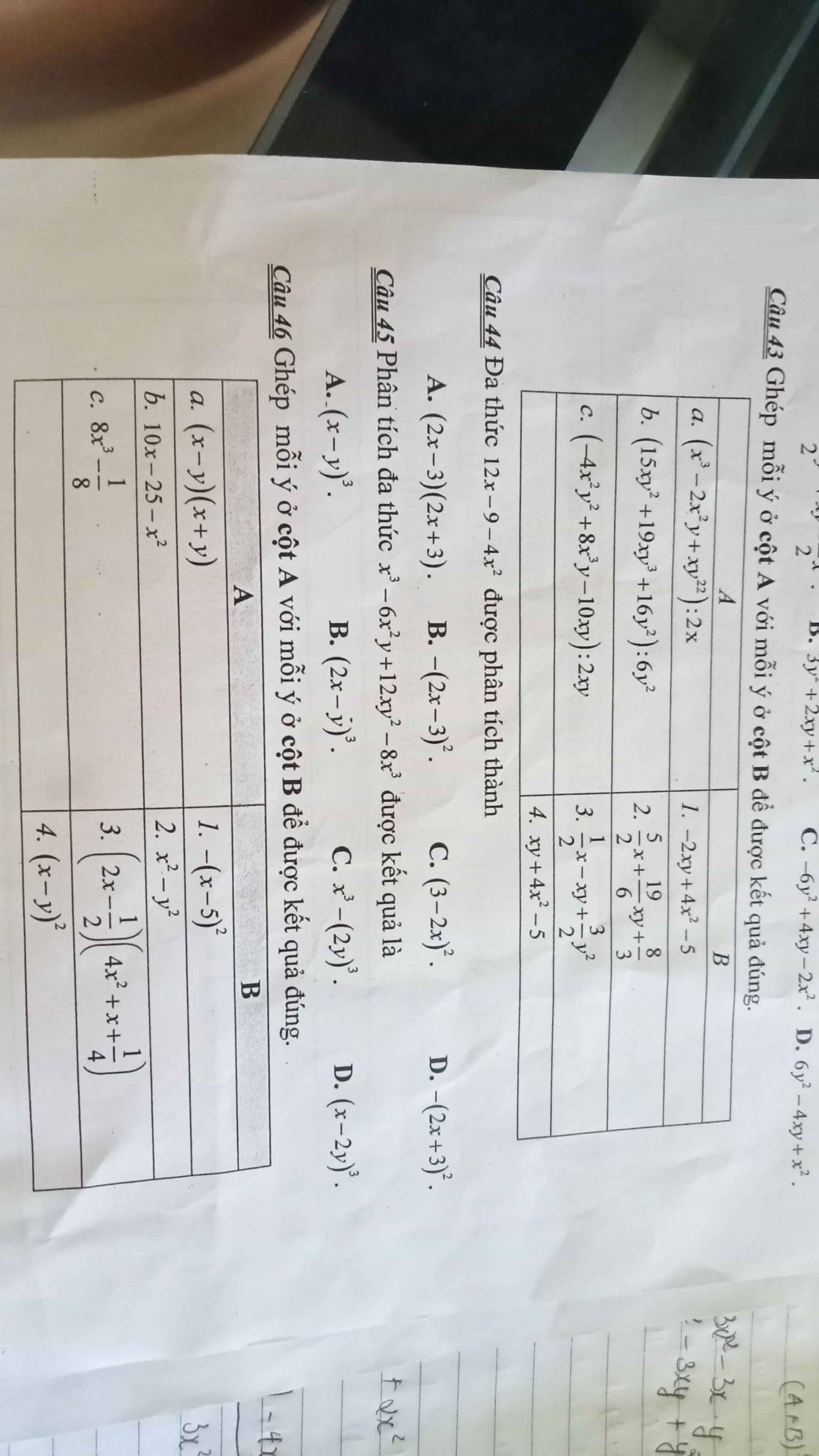
Câu 44:
\(12x-9-4x^2=-4x^2+12x-9=-\left(4x^2-12x+9\right)\)
\(=\left[\left(2x\right)^2-2\cdot3\cdot2x+3^2\right]=-\left(2x-3\right)^2\)
⇒ Chọn C
Câu 45:
\(x^3-6x^2y+12xy^2-8y^3=x^3-3\cdot2y\cdot x^2+3\cdot\left(2y\right)^2-\left(2y\right)^3\)
\(=\left(x-2y\right)^3\)
⇒ Chọn D
GH
27 tháng 6 2023
5
\(=4^2-x^2=\left(4-x\right)\left(4+x\right)\)
6
\(=4^2-\left(3x+1\right)^2=\left(4-3x-1\right)\left(4+3x+1\right)=\left(3-3x\right)\left(5+3x\right)\\ =3\left(1-x\right)\left(5+3x\right)\)
7
\(=\left(2x+5\right)^2-\left(3x\right)^2=\left(2x+5+3x\right)\left(2x+5-3x\right)\\ =\left(5x+5\right)\left(5-x\right)\\ =5\left(x+1\right)\left(5-x\right)\)
8
\(=\left(2x-1-3x+1\right)\left(2x-1+3x-1\right)=\left(-x\right)\left(5x-2\right)\)
9
\(=\left(2x\right)^2-2.2x.y+y^2=\left(2x-y\right)^2\)
10
\(=\left(x+1\right)^2-\left(3y\right)^2=\left(x+1-3y\right)\left(x+1+3y\right)\)
11
\(=\left(x^2y^2\right)^2+2.2x^2y^2+2^2=\left(x^2y^2+2\right)\)
12
\(=\left(y-2\right)^2-x^2=\left(y-2-x\right)\left(y-2+x\right)\)
13
\(=1-\left(3\sqrt{3}x\right)^3=\left(1-3\sqrt{3}x\right)\left[1^2+3\sqrt{3}.x+\left(3\sqrt{3}.x\right)^2\right]=\left(1-3\sqrt{3}x\right)\left(1+3\sqrt{3}x+27x^2\right)\)
H9
HT.Phong (9A5)
CTVHS
27 tháng 6 2023
Bài 5:
a) \(M=\left(2x-1\right)^2+2\left(2x-1\right)\left(3x+1\right)+\left(3x+1\right)^2\)
\(M=\left[\left(2x-1\right)+\left(3x+1\right)\right]^2\)
\(M=\left(5x\right)^2\)
Thay \(x=-\dfrac{1}{5}\) vào biểu thức M ta có:
\(\left(5\cdot-\dfrac{1}{5}\right)^2=\left(-1\right)^2=1\)
Vậy: ...
b) \(N=\left(3x-1\right)^2-2\left(9x^2-1\right)+\left(3x+1\right)^2\)
\(N=\left(3x-1\right)^2-2\left(3x+1\right)\left(3x-1\right)+\left(3x+1\right)^2\)
\(N=\left[\left(3x-1\right)-\left(3x+1\right)\right]^2\)
\(N=\left(-2\right)^2=4\)
Vậy: ...
28 tháng 6 2023
14: =x^3-3x^2+3x-1-1
=(x-1)^3-1
=(x-1-1)(x^2-2x+1+x-1+1)
=(x-2)(x^2-x+1)
15: =x^3+x^2-4x^2-4x+7x+7
=(x+1)(x^2-4x+7)
16: =2x^3-x^2-2x^2+x+2x-1
=(2x-1)(x^2-x+1)
28 tháng 6 2023
1: =x^2-2*x*2y+4y^2
=(x-2y)^2
2: 9x^2-y^2=(3x-y)(3x+y)
5: x^3-8=(x-2)(x^2+2x+4)
4: =x^2-(y-2)^2
=(x-y+2)(x+y-2)
7: 8x^3+12x^2+6x+1=(2x+1)^3
14: =x^3-3x^2+3x-1-1
=(x-1)^3-1
=(x-1-1)(x^2-2x+1+x-1+1)
=(x-2)(x^2-x+1)
15: =x^3+x^2-4x^2-4x+7x+7
=(x+1)(x^2-4x+7)
16: =2x^3-x^2-2x^2+x+2x-1
=(2x-1)(x^2-x+1)
KV
28 tháng 6 2023
a) (x + 2)³ + 1
= (x + 2)³ + 1³
= [(x + 2) + 1][(x + 2)² - (x + 2).1 + 1²]
= (x + 3)(x² + 4x + 4 - x - 2 + 1)
= (x + 3)(x² + 3x + 3)
b) x³ + 6x² + 12x + 9
= x³ + 3x² + 3x² + 9x + 3x + 9
= (x³ + 3x²) + (3x² + 9x) + (3x + 9)
= x²(x + 3) + 3x(x + 3) + 3(x + 3)
= (x + 3)(x² + 3x + 3)
c) x³ + 6x² + 12x + 7
= x³ + x² + 5x² + 5x + 7x + 7
= (x³ + x²) + (5x² + 5x) + (7x + 7)
= x²(x + 1) + 5x(x + 1) + 7(x + 1)
= (x + 1)(x² + 5x + 7)
d) 2x³ + 6x² + 12x + 8
= 2(x³ + 3x² + 6x + 4)
= 2(x³ + x² + 2x² + 2x + 4x + 4)
= 2[(x³ + x²) + (2x² + 2x) + (4x + 4)]
= 2[x²(x + 1) + 2x(x + 1) + 4(x + 1)]
= 2(x + 1)(x² + 2x + 4)
28 tháng 6 2023
VD2:
a: \(3-x^2=\left(\sqrt{3}-x\right)\left(\sqrt{3}+x\right)\)
b: 3-(x+1)^2
\(=\left(\sqrt{3}-x-1\right)\left(\sqrt{3}+x+1\right)\)
c: (x+5)^2-4x^2
=(x+5+2x)(x+5-2x)
=(-x+5)(3x+5)
d: (x+1)^2-(2x-1)^2
=(x+1+2x-1)(x+1-2x+1)
=(2-x)*3x
H9
HT.Phong (9A5)
CTVHS
28 tháng 6 2023
Bài 6:
a) \(P=27-27a+9x^2-x^3\)
\(P=3^3-3\cdot3^2\cdot x+3\cdot3\cdot x^2-x^3\)
\(P=\left(3-x\right)^3\)
Thay \(x=-17\) vào P ta được:
\(\left(3--17\right)^3=20^3=8000\)
Vậy: ...
b) \(Q=x^3+3x^2+3x\)
\(Q=x^3+3x^2+3x+1-1\)
\(Q=\left(x+3\right)^3-1\)
Thay \(x=99\) vào Q ta có:
\(\left(99+1\right)^3-1=100^3-1=1000000-1=999999\)
Vậy: ...
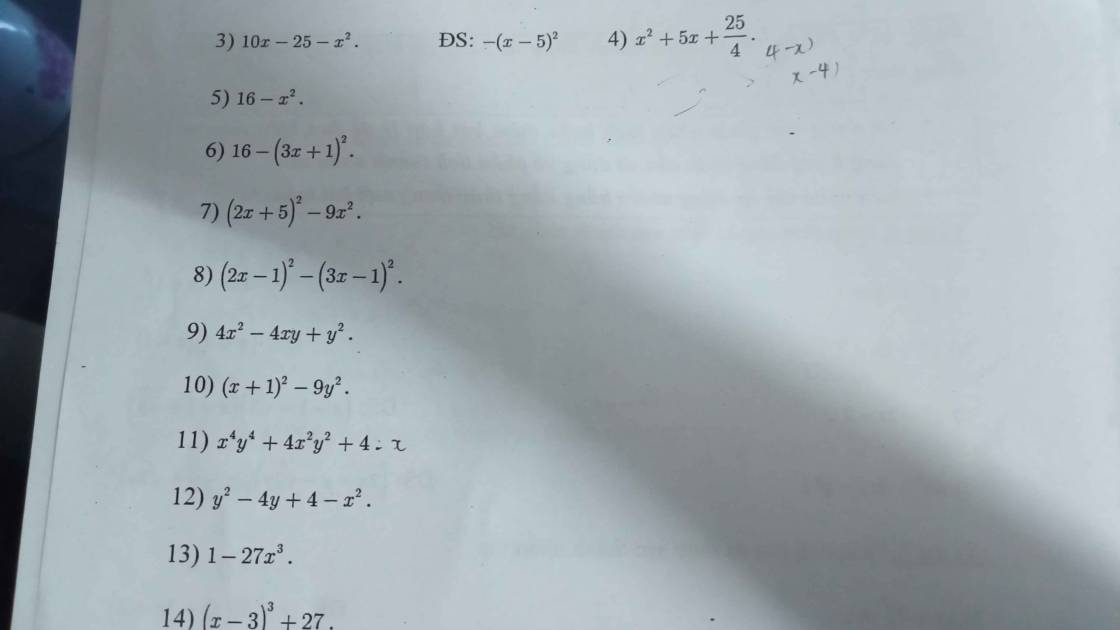
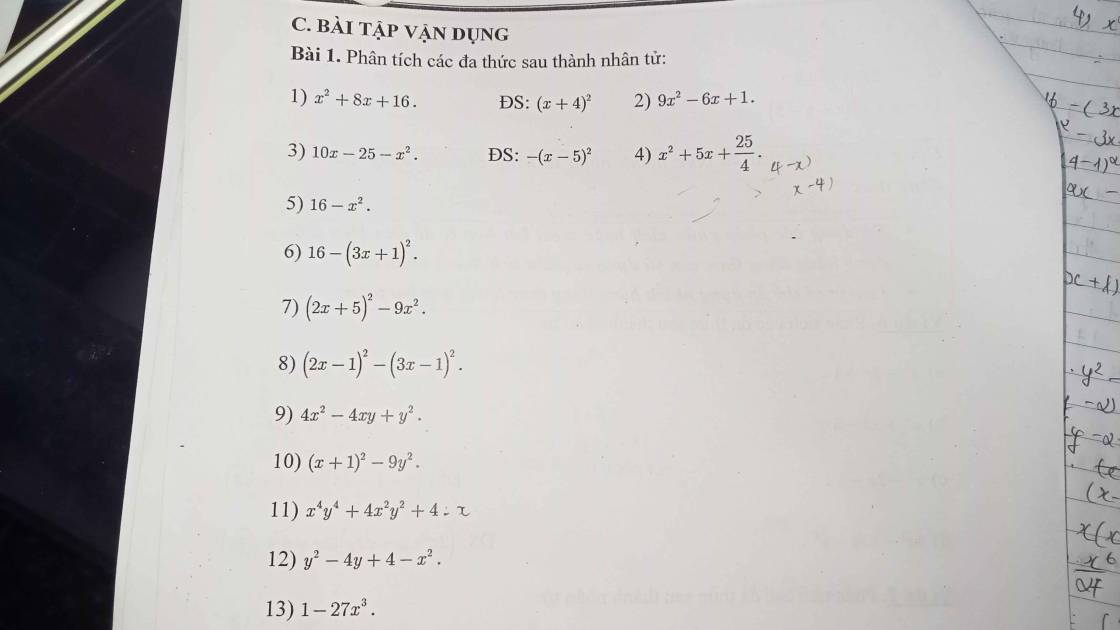
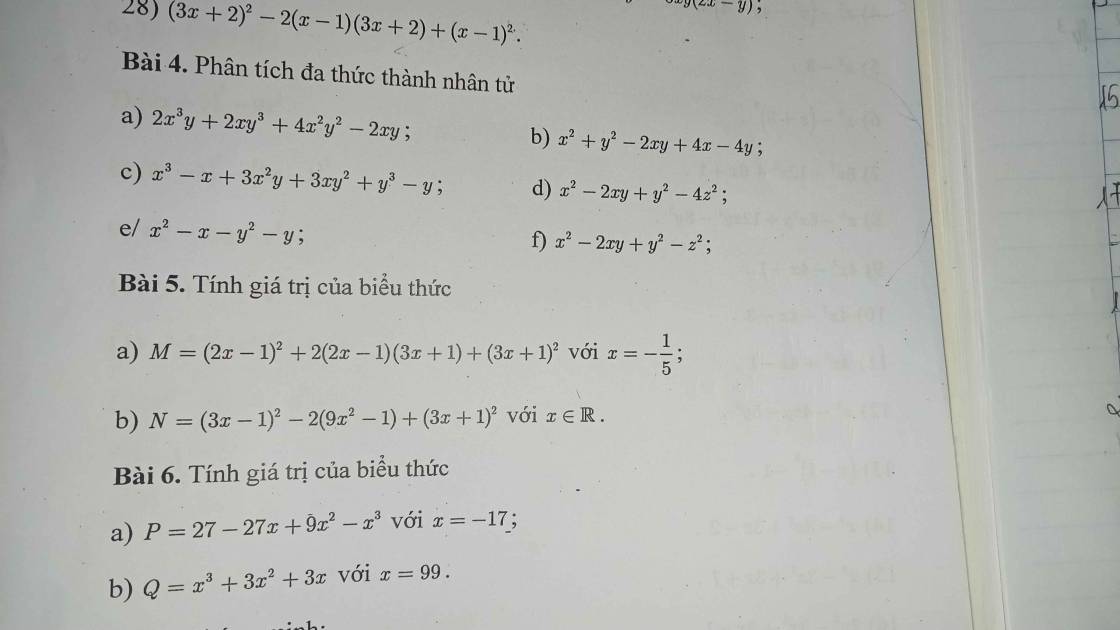
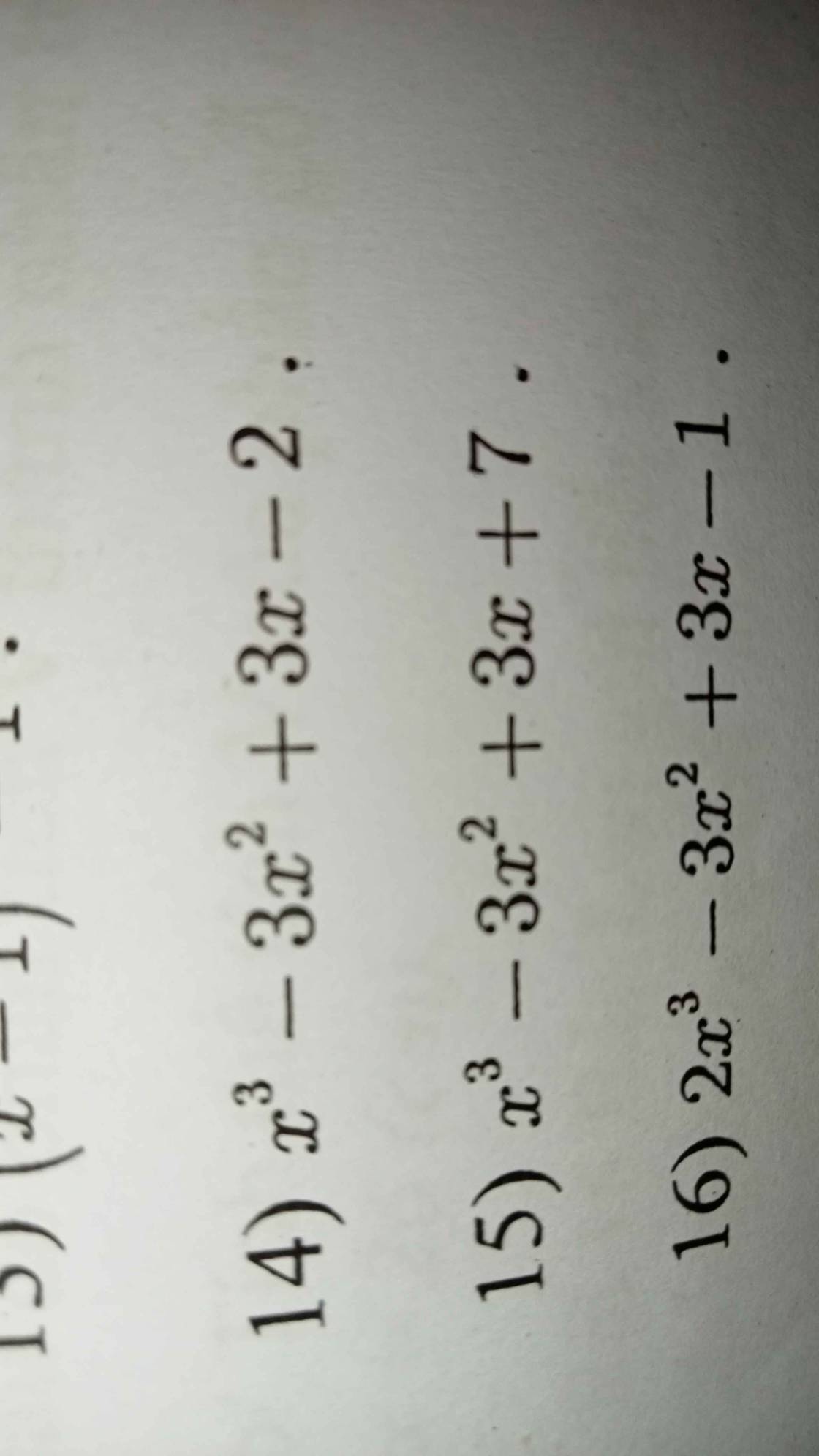
Ch
ỉ cần vt cho mik vd thôi ạ