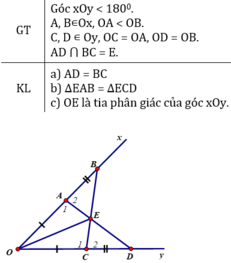
cho góc xOy khác góc bẹt. lấy điểm A và B thuộc tia Ox, C và D thuộc tia Oy sao cho OA = OC; OB = OD
a) Chứng minh AD = BC
b) chứng minh tam giác IAB = tam giác ICB
c) Chứng minh OI là tia phân giác của xOy
d) Chứng minh AC song song BD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ΔAEB = ΔCED ⇒ EA = EC (hai cạnh tương ứng)
ΔOAE và ΔOCE có
OA = OC
EA = EC
OE cạnh chung
⇒ ΔOAE = ΔOCE (c.c.c)
⇒  (hai góc tương ứng)
(hai góc tương ứng)
Vậy OE là tia phân giác của góc xOy.

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy

ΔOAD và ΔOCB có:
OA = OC (gt)
Góc O chung
OD = OB (gt)
⇒ ΔOAD = ΔOCB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng).

Do ΔOAD = ΔOCB (chứng minh trên)
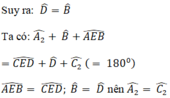
OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
Xét ΔAEB và ΔCED có:
∠B = ∠D
AB = CD
∠A2 = ∠C2
⇒ΔAEB = ΔCED (g.c.g)

a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB

Xét ΔODB có
\(\dfrac{OA}{OB}=\dfrac{OC}{OD}\)
Do đó: AC//BD

a)
ΔOAD và ΔOCB có:
OA = OC (gt)
Góc O chung
OD = OB (gt)
⇒ ΔOAD = ΔOCB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng).
c) Ta có:
ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: BOE=DOE
hay OE là tia phân giác của góc xOy

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC

a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{COB}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOCB
nên \(\widehat{OAD}=\widehat{OCB}\)
mà \(\widehat{MAB}=180^0-\widehat{OAD}\)
và \(\widehat{MCD}=180^0-\widehat{OCB}\)
nên \(\widehat{MAB}=\widehat{MCD}\)
Xét ΔMAB và ΔMCD có
\(\widehat{MAB}=\widehat{MCD}\)
AB=CD
\(\widehat{MBA}=\widehat{MDC}\)
Do đó: ΔMAB=ΔMCD

Ta có hình vẽ:
x O y A B C D E
a/ Xét tam giác OAD và tam giác OBC có:
OA = OC (GT)
\(\widehat{O}\): góc chung
OB = OD (GT)
=> tam giác OAD = tam giác OBC (c.g.c)
=> AD = BC (2 cạnh tương ứng)
b/ Ta có: \(\widehat{B}\)=\(\widehat{D}\) (vì tam giác OAD = tam giác OBC) (1)
Ta có: \(\begin{cases}OA=OC\\OB=OD\end{cases}\)\(\Rightarrow AB=CD\) (2)
Ta có: \(\widehat{OAD}\)=\(\widehat{OCB}\) (vì tam giác OAD = tam giác OBC) (*)
+)Ta có: \(\widehat{OAD}\)+\(\widehat{DAB}\)=1800 (**)
+) Ta có: \(\widehat{OCB}\)+\(\widehat{BCD}\)=1800 (***)
Từ (*),(**),(***) => \(\widehat{DAB}\)=\(\widehat{BCD}\) (3)
Từ (1),(2),(3) => tam giác EAB = tam giác ECD
c/ Xét tam giác OAE và tam giác OCE có:
OA = OC (GT)
AE = EC (vì tam giác EAB = tam giác ECD)
OE: cạnh chung
=> tam giác OAE = tam giác OCE (c.c.c)
=> \(\widehat{AOE}\)=\(\widehat{COE}\) (2 góc tương ứng)
=> OE là phân giác \(\widehat{xOy}\) (đpcm)
a: Xét ΔOAD và ΔOCB có
OA=OC
góc O chung
OD=OB
Do đó: ΔOAD=ΔOCB
=>AD=CB
b: ΔOAD=ΔOCB
=>góc OAD=góc OCB và góc OBC=góc ODA
=>góc IAB=góc ICD
Xét ΔIAB và ΔICD có
góc IAB=góc ICD
AB=CD
góc IBA=góc IDC
Do đó: ΔIAB=ΔICD
c: Xét ΔOAI và ΔOCI có
OA=OC
AI=CI
OI chung
Do đó: ΔOAI=ΔOCI
=>góc AOI=góc COI
=>OI là phân giác của góc AOC
d: Xét ΔOBD có OA/OB=OC/OD
nên AC//BD