Hãy tính khoảng cách \(BC\) trong phần câu hỏi khởi động trang 52.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Giao diện của GIMP khá khác biệt so với các phần mềm khác mà bạn có thể đã sử dụng trước đó. GIMP có giao diện chính gồm một cửa sổ chính, chứa các thanh công cụ và menu, cùng với một cửa sổ xem trước và xử lý hình ảnh. Giao diện của GIMP có thể được tùy chỉnh để hiển thị hoặc ẩn các thanh công cụ và menu, cho phép người dùng tùy chỉnh giao diện theo cách thích hợp nhất với nhu cầu của mình.
2: Có, bạn có thể mở một ảnh trong GIMP bằng cách nhấn vào nút "Open" trong menu "File" hoặc sử dụng tổ hợp phím Ctrl+O trên bàn phím. Sau đó, bạn có thể phóng to hoặc thu nhỏ ảnh bằng cách sử dụng các công cụ phóng to và thu nhỏ có sẵn trong thanh công cụ của GIMP. Các công cụ này bao gồm: "Scale Tool" (công cụ tỷ lệ), "Zoom Tool" (công cụ phóng to), "Shrink Tool" (công cụ thu nhỏ) và "Crop Tool" (công cụ cắt).

Gọi giá tiền đôi giày lúc chưa giảm giá là \(x\) (đồng). Điều kiện: \(x > 0\).
Sau khi giảm giá \(15\% \) thì giá mới của đôi giày bằng \(85\% \) giá ban đầu của đôi giày. Ta có phương trình:
\(x.85\% = 1275000\)
\(x = 1275000:85\% \)
\(x = 1500000\) (thỏa mãn)
Vậy giá của đôi giày khi chưa giảm giá là 1 500 000 đồng.

Ta có: \(OA = OB = 120:2 = 60\)
Xét tam giác OBB’ có:
\(\sin \widehat {BOB'} = \frac{{BB'}}{{OB}} = \frac{{27}}{{60}} = \frac{9}{{20}}\)
\(\widehat {AOC} = 2\widehat {BOB'}\)
(Vì số đo cung AC gấp 2 lần số đo cung AB)
Xét tam giác OCC’ vuông tại C’ có:
\(\begin{array}{l}\sin \widehat {COC'} = \frac{{CC'}}{{OC}}\\ \Leftrightarrow CC' = OC.\sin \widehat {COC'} = OC.\sin \left( {2\widehat {BOB'}} \right)\end{array}\)
Mà \(\sin \left( {2\widehat {BOB'}} \right) = 2.\sin \widehat {BOB'}.cos\widehat {BOB'}\)
\( = 2.\frac{9}{{20}}.\frac{{\sqrt {319} }}{{20}} = \frac{{9\sqrt {319} }}{{400}}\)
Vậy khoảng cách từ C đến AH là \(60.\frac{{9\sqrt {319} }}{{200}} \approx 48,2cm\).
 trên màn hình máy tính và trả lời các câu hỏi sau:
trên màn hình máy tính và trả lời các câu hỏi sau: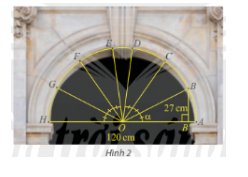
Xét ΔABC có D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình
=>DE=1/2BC
=>BC=2DE=90(m)
Vì \(BD = DA \Rightarrow D\) là trung điểm của \(AB\);
Vì \(EC = EA \Rightarrow E\) là trung điểm của \(AC\).
Do đó, \(DE\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow \left\{ \begin{array}{l}DE//BC\\DE = \frac{1}{2}BC\end{array} \right.\) (tính chất đường trung bình).
\( \Rightarrow 45 = \frac{1}{2}BC \Leftrightarrow BC = 45.2 = 90\left( m \right)\)
Vậy khoảng các của hai điểm \(B\) và \(C\) là 90 m.