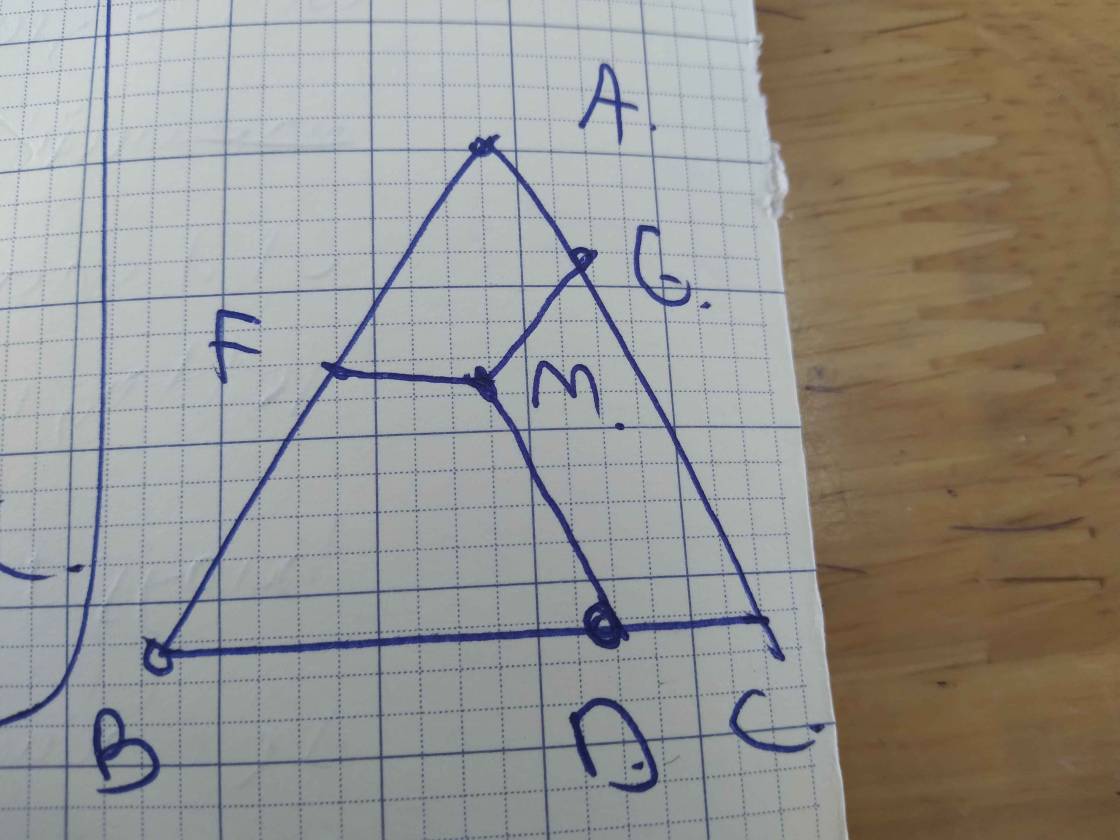
Cho tam giác ABC.Điểm I nằm trong tam giác. Từ I kẻ các đường song song với BC;CA;AB lần lượt cắt các cạnh AB;BC;CA tại M;N;P.Nối AN;CM;BP.Chúng cắt nhau tại các điểm E;F;K.Hãy chứng tỏ tổng dt các tam giác ENC;FPA;KMB bằng dt tam giác EFK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì điểm I cách đều ba cạnh của tam giác ABC và nằm trong tam giác nên I là giao điểm của ba đường phân giác của tam giác ABC, tức là BI, CI lần lượt là tia phân giác của góc N và góc C. Do EF // BC nên ∠B1= ∠I1(so le trong), suy ra ∠I2 = ∠B2 .
Suy ra: BI, CI lần lượt là tia phân giác của góc B và góc C.
Do EF // BC nên ∠B1 = ∠BIE (so le trong).
Lại có: ∠B1 = ∠B2 ( vì BI là tia phân giác của góc B )
Suy ra: ∠B2 = ∠BIE
Vậy EF = EI + IF = BE + CF.

a) Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔABE∼ΔACF(g-g)

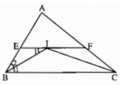
A B C E F I 1 2 1
Vì điểm I cách đều ba cạnh của tam giác ABC và nằm trong tam giác nên I là giao điểm của ba đường phân giác của tam giác ABC, tức BI, CI lần lượt là tia phân giác của góc B và góc C. Do EF // BC nên \(\widehat{B_1}=\widehat{I_1}\) (hai góc so le trong), suy ra \(\widehat{I_1}=\widehat{B_2}\). Vậy tam giác EBI cân tại E, tức là EI = EB. Tương tự ta có FI = FC.
Vậy EF = EI + IF = BE + CF.