So sánh số hữu tỉ \(\frac{a}{b}\)với số 0 khi a,b cùng dấu & khi a,b khác dấu.
Giúp mik nha!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
1
10 tháng 6 2016
Khi a,b cùng dấu thì \(\frac{a}{b}>0\) ; khác dấu thì \(\frac{a}{b}< 0\)
PT
1
CM
22 tháng 10 2017
Với a, b ∈ Z; b ≠ 0 thì:
- Khi a, b cùng dấu thì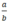 
> 0
- Khi a, b khác dấu thì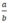 
< 0
Tổng quát: Số hữu tỉ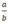 
(a, b ∈ Z; b ≠ 0) > 0 nếu a, b cùng dấu; < 0 nếu a, b khác dấu; = 0 nếu a = 0.
7 tháng 9 2020
https://olm.vn/hoi-dap/detail/262047614383.html . E tham khảo nha :))
V
2
25 tháng 8 2015
Khi a,b cùng dấu thì \(\frac{a}{b}\)>0 với a,b\(\ne\)0
Và a,b khác dấu thì \(\frac{a}{b}\)<0 với a,b\(\ne\)0
25 tháng 6 2016
Khi a, b cùng dấu thì \(\frac{a}{b}>0\)
Khi a, b khác dấu thì \(\frac{a}{b}< 0\)
NK
2
H
6 tháng 9 2021
Nếu a,b cùng dấu thì \(\dfrac{a}{b}\ge0\)
Nếu a,b khác dấu thì \(\dfrac{a}{b}< 0\)
6 tháng 9 2021
\(\left[{}\begin{matrix}a\ge0,b>0\\a\le0,b< 0\end{matrix}\right.\Rightarrow\dfrac{a}{b}\ge0\\ \left[{}\begin{matrix}a\ge0,b< 0\\a\le0,b>0\end{matrix}\right.\Rightarrow\dfrac{a}{b}\le0\)
LH
2
khi a, b cùng dấu
TH1 : a,b >0 \(\Rightarrow\frac{a}{b}>0\)TH2 :a,b <0 \(\frac{\left(-a\right)}{\left(-b\right)}=\frac{a}{b}>0\)
khi a, b khác dấu
TH1 : a>0 ; b<0 => \(\frac{a}{-b}< 0\)TH2 : a<0 ; b>0 => \(\frac{\left(-a\right)}{b}< 0\)
Có trường hợp a = 0 ko bạn ?