a) S:" ∃x ∈ IR, x^2 = 5x - 4"
b) P:"∃x ∈ IR, 2x + 1=0"
Xét tính đúng sai và viết mệnh đề phủ định của nó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) Mệnh đề sai, vì \(x = 0 \in \mathbb{R}\) nhưng \({0^2}\) không lớn hơn 0.
Mệnh đề phủ định của mệnh đề này là: “\(\exists x \in \mathbb{R},{x^2} \le 0\)”
b) Mệnh đề đúng, vì \(x = 1 \in \mathbb{R}\) thỏa mãn \({1^2} = 5.1 - 4\)
Mệnh đề phủ định của mệnh đề này là: “\(\forall x \in \mathbb{N},{x^2} \ne 5x - 4\)”
c) Mệnh đề sai, vì \(2x + 1 = 0 \Leftrightarrow x = - \frac{1}{2} \notin \mathbb{Z}\)
Mệnh đề phủ định của mệnh đề này là: “\(\forall x \in \mathbb{Z},2x + 1 \ne 0\)”
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) Mệnh đề sai, vì chỉ có \(x = - 3\) thảo mãn \(x + 3 = 0\) nhưng \( - 3 \notin \mathbb{N}\).
Mệnh đề phủ định của mệnh đề này là: “\(\forall x \in \mathbb{N},x + 3 \ne 0\)”.
b) Mệnh đề đúng, vì \({(x - 1)^2} \ge 0\) hay\({x^2} + 1 \ge 2x\) với mọi số thực x.
Mệnh đề phủ định của mệnh đề này là: “\(\exists x \in \mathbb{R},{x^2} + 1 < 2x\)”
c) Mệnh đề sai, vì có \(a = - 2 \in \mathbb{R},\sqrt {{{( - 2)}^2}} = 2 \ne a\)
Mệnh đề phủ định của mệnh đề này là: “\(\exists a \in \mathbb{R},\sqrt {{a^2}} \ne a\)”.
CM
1 tháng 9 2019
C: “∀ x ∈ R : x < x + 1”.
C− : “∃ x ∈ R: x ≥ x + 1”.
C− sai vì x + 1 luôn lớn hơn x.
PT
1
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Phủ định của mệnh đề “\(\forall x \in \mathbb{R},\;{x^2} \ne 2x - 2\)” là mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} = 2x - 2\)”
Mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} = 2x - 2\)” sai vì \({x^2} \ne 2x - 2\)với mọi số thực x ( vì \({x^2} - 2x + 2 = {(x - 1)^2} + 1 > 0\) hay \({x^2} > 2x - 2\)).
b) Phủ định của mệnh đề “\(\forall x \in \mathbb{R},\;{x^2} \le 2x - 1\)” là mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} > 2x - 1\)”
Mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} > 2x - 1\)” đúng vì có \(x = 2 \in \mathbb{R}:{2^2} > 2.2 - 1\) hay \(4 > 3\) (luôn đúng).
c) Phủ định của mệnh đề “\(\exists x \in \mathbb{R},\;x + \frac{1}{x} \ge 2\)” là mệnh đề “\(\forall x \in \mathbb{R},\;x + \frac{1}{x} < 2\)”.
Mệnh đề “\(\forall x \in \mathbb{R},\;x + \frac{1}{x} < 2\)” sai vì \(x = 2 \in \mathbb{R}\) nhưng \(x + \frac{1}{x} = 2 + \frac{1}{2} > 2\).
d) Phủ định của mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} - x + 1 < 0\)” là mệnh đề “\(\forall x \in \mathbb{R},\;{x^2} - x + 1 \ge 0\)”.
Mệnh đề “\(\forall x \in \mathbb{R},\;{x^2} - x + 1 \ge 0\)” đúng vì \({x^2} - x + 1 = {\left( {x - \frac{1}{2}} \right)^2} + \frac{3}{4} \ge 0\) với mọi số thực x.
PT
1
CM
19 tháng 1 2019
B: “∃ x ∈ Q : x2 = 2”.
B− : “∀ x ∈ Q : x2 ≠ 2”
B− đúng.
Lưu ý: √2 là số vô tỷ.
CM
9 tháng 10 2018
D: “∃ x ∈ R: 3x = x2 + 1”
D− : “∀ x ∈ R ; 3x ≠ x2 + 1”
D− sai vì với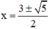 
D− thỏa mãn:
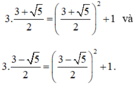
a: S: "\(\exists x\in R,x^2=5x-4\)"
x^2=5x-4
=>x^2-5x+4=0
=>(x-1)(x-4)=0
=>x=1 hoặc x=4
=>Mệnh đề này đúng
Mệnh đề phủ định là: \(\overline{S}:"\forall x\in R,x^2\ne5x-4"\)
b: \(P:"\exists x\in R,2x+1=0"\)
2x+1=0
=>2x=-1
=>\(x=-\dfrac{1}{2}\)
=>Mệnh đề này đúng
Mệnh đề phủ định là:
\(\overline{P}:"\forall x\in R,2x+1\ne0"\)