Một xe khách khởi hành từ bến xe phía Bắc bưu điện thành phố Nha Trang để đi ra thành phố Đà Nẵng với tốc độ 40 km/h (Hình 2).

a) Biết rằng bến xe cách bưu điện thành phố Nha Trang 6 km. Sau \(x\) giờ, xe khách cách bưu điện thành phố Nha Trang \(y\)km. Tính \(y\) theo \(x\).
b) Chứng minh rằng \(y\) là một hàm số bậc nhất theo biến \(x\).
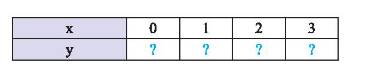
c) Hoàn thành bảng giá trị của hàm số ở câu b) và giải thích ý nghĩa của bảng giá trị này:


a) Quãng đường xe khách đi được sau \(x\) giờ với vận tốc 40 km/h là \(40.x\) (km)
Vì ban đầu bến xe cách bưu điện Nha Trang 6 km nên sau \(x\) giờ xe khách cách bưu điện thành phố Nha Trang số km là: \(40x + 6\). Do đó, \(y = 40x + 6\) với \(y\) là số km xe khách cách bưu điện thành phố Nha Trang sau \(x\) giờ.
b) Vì hàm số \(y = 40x + 6\) có dạng \(y = ax + b\) với \(a = 40;b = 6\) nên \(y\) là một hàm số bậc nhất theo biến \(x\).
c)
- Với \(x = 0 \Rightarrow y = f\left( 0 \right) = 40.0 + 6 = 6\);
- Với \(x = 1 \Rightarrow y = f\left( 1 \right) = 40.1 + 6 = 46\);
- Với \(x = 2 \Rightarrow y = f\left( 2 \right) = 40.2 + 6 = 86\);
- Với \(x = 3 \Rightarrow y = f\left( 3 \right) = 40.3 + 6 = 126\);
Ta có bảng sau:
\(x\)
0
1
2
3
\(y\)
6
46
86
126
Bảng này thể hiện khoảng cách của xe khách so với bưu điện Nha Trang sau 0 giờ; 1 giờ; 2 giờ; 3 giờ.