2. không tính kết quả, hay so sánh:
a) A= 2022.2024 và B= 20232
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


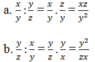
Kết quả câu b là nghịch đảo kết quả câu a.
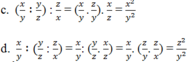
Kết quả câu c và d khác nhau. Phép chia không có tính chất giao hoán, tính chất kết hợp.

a)
Ta có:
\(c=25\times26261=25\times\left(26260+1\right)=25\times10\times26\times101+25\)
\(d=26\times25251=26\times\left(25250+1\right)=26\times10\times25\times101+26\)
Vì \(25\times10\times26\times101\) = \(26\times10\times25\times101\) mà \(25< 26\)
=> \(c< d\)
b)
Ta có:
\(b=2022\times2024=2022\times\left(2023+1\right)=2022\times2023+2022\)
\(a=2023\times2023=2023\times\left(2022+1\right)=2023\times2022+2023\)
Vì \(2022\times2023=2023\times2022\) mà \(2022< 2023\)
=> \(b< a\)

a)A=(1996+2).(2000-2)
A=1996.2000-1996.2+2000.2-4
A=1996.2000+4
=>A>B

b) \(M=\dfrac{10^{2023}+1}{10^{2024}+1}< 1\) ( Vì tử < mẫu )
Ta có: \(M=\dfrac{10^{2023}+1}{10^{2024}+1}< \dfrac{10^{2023}+1+9}{10^{2024}+1+9}=\dfrac{10^{2023}+10}{10^{2024}+10}=\dfrac{10.\left(10^{2022}+1\right)}{10.\left(10^{2023}+1\right)}=\dfrac{10^{2022}+1}{10^{2023}+1}=N\)
Vì \(\dfrac{10^{2023}+1}{10^{2024}+1}< \dfrac{10^{2022}+1}{10^{2023}+1}\) nên \(M< N\)


a = 2011.2013
a = 2011.(2012+1)
a = 2011.2012 + 2011
b = 2012.2012
b = (2011+1).2012
b = 2011.2012 + 2012
Vì 2011 < 2012
=> 2011.2012 + 2011 < 2011.2012 + 2012
=> a < b

\(B=2018.2022=\left(2020-2\right)\left(2020+2\right)=2020^2-2.2020+2.2020-2.2\)
\(=A-4< A\).

A= 2013. ( 2021 + 1 ) = 2013 . 2012 + 2013
B = 2012 . 2014 = 2012 . ( 2013 + 1 ) = 2012 . 2013 + 2012
Vì 2013 > 2012 ==> A > B
\(Bài.2:\\ A=2022.2024=\left(2023-1\right).\left(2023+1\right)=2023^2-1^2\\ Vì:2023^2-1^2< 2023^2\Rightarrow2022.2024< 2023^2\\ Vậy:A< B\)
câu b ai trả lời nhỉ?