cho tam giác abc ko vuông các đường trung trực của ab và ac cắt nhau tại o cắt bc lần lượt tại m và n.CMR AO là pg của góc MAN
Minh đang cần gấp ai giải đc mik hậu tạ 50k
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 2 2018
Theo bài 8.3 ta đã có ∠A1 = ∠B1 , ∠A2 = ∠C2 (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra ∠(OAB) = ∠(OBA) , ∠(OAC) = ∠(OCA) , ∠(OBC) = ∠(OCB) . Kết hợp với(1) ∠(OBM) = ∠(OAM) , ∠(OCN) = ∠(OAN) , hay ∠(OAM) = ∠(OBC) = ∠(OCB) = ∠(OAN). Vậy OA là tia phân giác góc MAN.
TP
14 tháng 12 2017
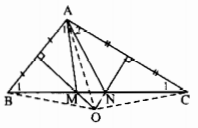
Theo bài 8.3 ta đã có\(\widehat{A_1} =\widehat{B}_1;\widehat{A_2}=\widehat{C_1} \) (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra \(\widehat{OAB}=\widehat{OBA},\widehat{OAC}=\widehat{OCA},\widehat{OCB}=\widehat{OBC}\)Kết hợp với (1) \(\widehat{OBM}=\widehat{OAM},\widehat{OCN}=\widehat{OAN}\) hay\(\widehat{OAM}=\widehat{OBC}=\widehat{OCB}=\widehat{OAN}\) . Vậy OA là tia phân giác góc MAN.
17 tháng 12 2017
Hình thì bạn kia vẽ rồi nên mình không vẽ nữa nha
Theo bài 8.3 ta đã cóˆA1=ˆB1;ˆA2=ˆC1A1^=B^1;A2^=C1^ (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra ˆOAB=ˆOBA,ˆOAC=ˆOCA,ˆOCB=ˆOBCOAB^=OBA^,OAC^=OCA^,OCB^=OBC^Kết hợp với (1) ˆOBM=ˆOAM,ˆOCN=ˆOANOBM^=OAM^,OCN^=OAN^ hayˆOAM=ˆOBC=ˆOCB=ˆOANOAM^=OBC^=OCB^=OAN^ . Vậy OA là tia phân giác góc MAN.
23 tháng 8 2016
a)
Chứng minh
\(\Delta COE=\Delta AOE\left(c.g.c\right)\)
\(\Rightarrow OC=OA\)(hai cạnh tương ứng) \(\left(1\right)\)
\(\Delta BOD=\Delta AOD\left(c.g.c\right)\)
\(\Rightarrow OB=OA\)(hai cạnh tương ứng) \(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)suy ra \(OB=OC\)
vẽ hình ra mới giải được
ko bị hình mik bt vẽ