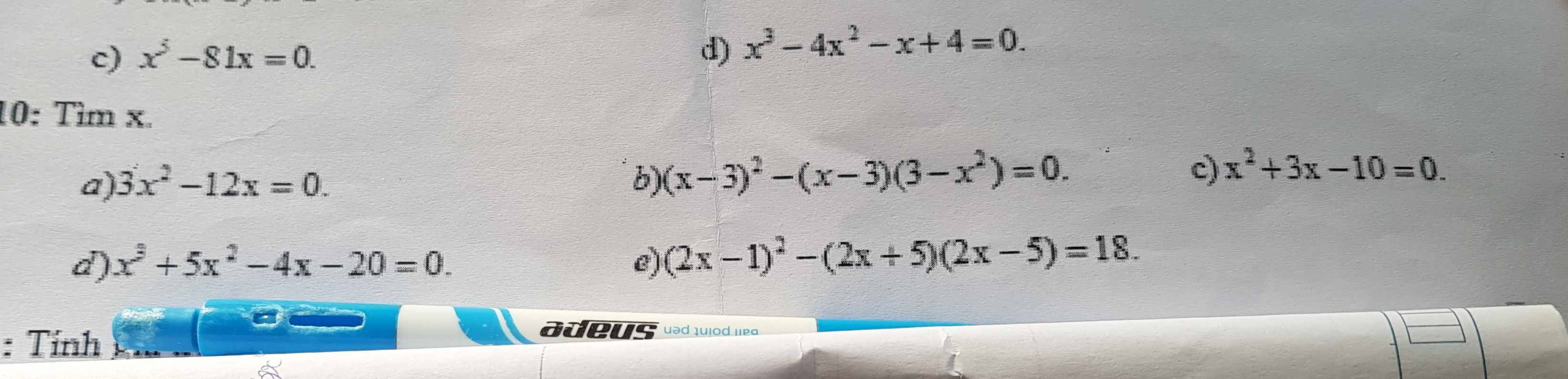Lm hộ e bài 8 vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
10 tháng 9 2023
Đúng(0)
Những câu hỏi liên quan
2 tháng 7 2023
a: \(P=\dfrac{a+1+\sqrt{a}}{a+1}:\dfrac{a+1-2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(a+1\right)}\)
\(=\dfrac{a+\sqrt{a}+1}{a+1}\cdot\dfrac{\left(a+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)^2}=\dfrac{a+\sqrt{a}+1}{\sqrt{a}-1}\)
b: P<1
=>P-1<0
=>\(\dfrac{a+\sqrt{a}+1-\sqrt{a}+1}{\sqrt{a}-1}< 0\)
=>căn a-1<0
=>0<a<1
c: Thay x=19-8căn3 vào P, ta được:
\(P=\dfrac{19-8\sqrt{3}+4+\sqrt{3}+1}{4+\sqrt{3}-1}=\dfrac{31-15\sqrt{3}}{2}\)
12 tháng 7 2021
Bài 8:
a) Ta có: AD+DB=AB(D nằm giữa A và B)
AE+EC=AC(E nằm giữa A và C)
mà DB=EC(gt)
và AB=AC(ΔABC cân tại A)
nên AD=AE
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
b) Xét ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(AD=AE;AB=AC\right)\)
Do đó: DE//BC(Định lí Ta lét đảo)
c) Xét tứ giác BDEC có DE//BC(cmt)
nên BDEC là hình thang có hai đáy là DE và BC(Định nghĩa hình thang)
Hình thang BDEC(DE//BC) có \(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
nên BDEC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
12 tháng 7 2021
Bài 7:
a) Xét ΔADE vuông tại E và ΔBCF vuông tại F có
AD=BC(ABCD là hình thang cân)
\(\widehat{B}=\widehat{C}\)(ABCD là hình thang cân)
Do đó: ΔADE=ΔBCF(Cạnh huyền-góc nhọn)
Suy ra: DE=CF(Hai cạnh tương ứng)
\(\Leftrightarrow DE+EF=CF+FE\)
\(\Leftrightarrow DF=CE\)
b) Xét tứ giác ABFE có
AE//BF(gt)
AE=BF(ΔAED=ΔBFC)
Do đó: ABFE là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Suy ra: AB=EF(Hai cạnh đối)
10 tháng 2 2022
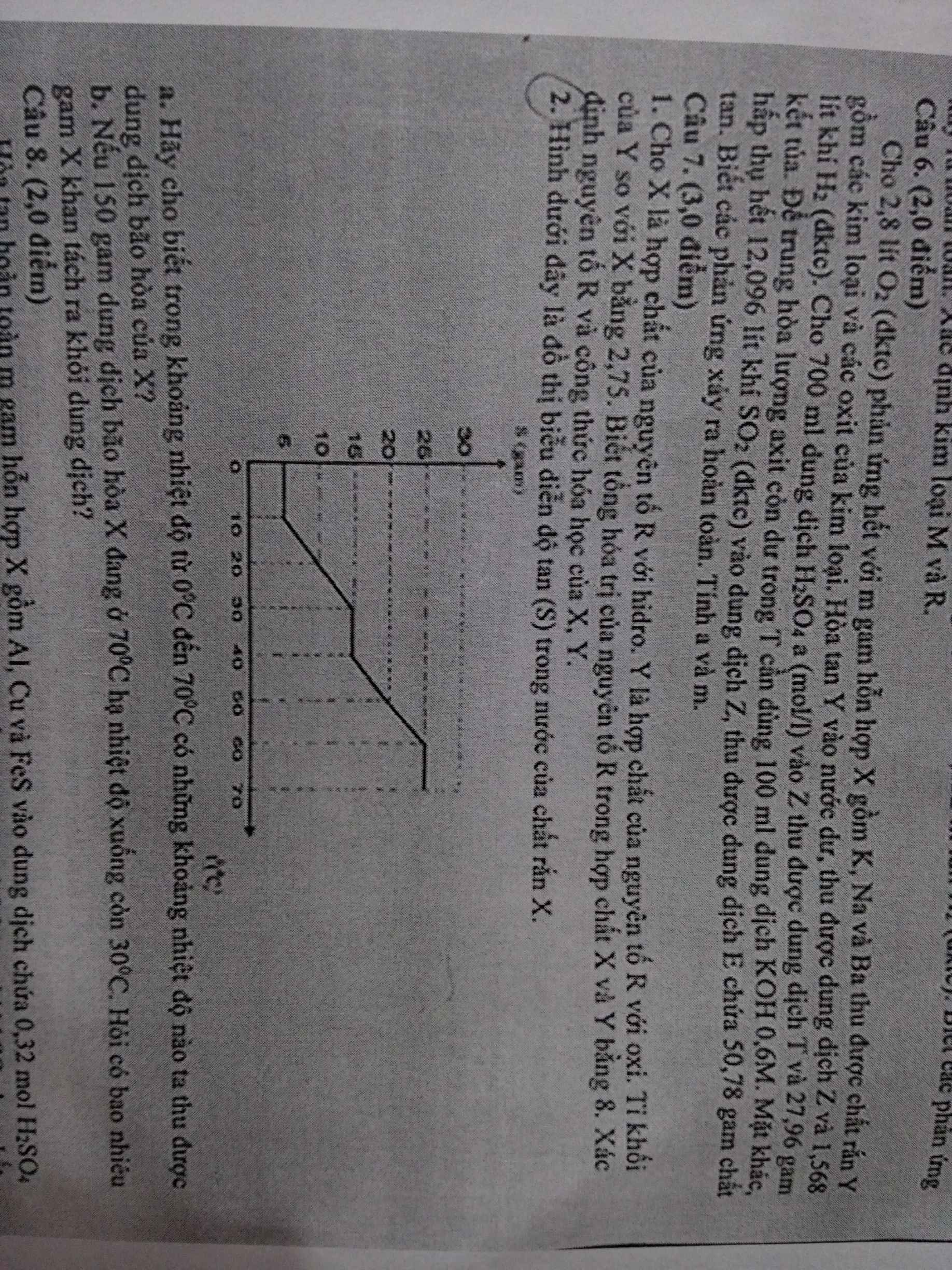
a) Những khoảng nhiệt độ mà dd X bão hòa:
+ 0-10oC
+ 30-40oC
+ 60-70oC
b)
- Xét khoảng 60-70oC:
Gọi khối lượng NaCl trong dd bão hòa tại khoảng nhiệt độ này là a (g)
\(S_{70^oC}=\dfrac{a}{150-a}.100=25\left(g\right)\)
=> a = 30 (g)
=> \(m_{H_2O}=150-30=120\left(g\right)\)
- Xét khoảng 30-40oC:
Gọi khối lượng NaCl trong dd bão hòa tại nhiệt độ này là b (g)
\(S_{30^oC}=\dfrac{b}{120}.100=15\)
=> b = 18 (g)
=> mNaCl(tách ra) = 30 - 18 = 12 (g)
19 tháng 2 2022
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
6 tháng 11 2021
a) \(\Rightarrow3x\left(x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
b) \(\Rightarrow\left(x-3\right)\left(x-3-3+x^2\right)=0\Rightarrow\left(x-3\right)\left(x-2\right)\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=2\\x=-3\end{matrix}\right.\)
c) \(\Rightarrow x\left(x-2\right)+5\left(x-2\right)=0\Rightarrow\left(x-2\right)\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\)
d) \(\Rightarrow x^2\left(x+5\right)-4\left(x+5\right)=0\Rightarrow\left(x+5\right)\left(x^2-4\right)=0\)
\(\Rightarrow\left(x+5\right)\left(x-2\right)\left(x+2\right)=0\)\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=2\\x=-2\end{matrix}\right.\)
e) \(\Rightarrow4x^2-4x+1-4x^2+25=18\)
\(\Rightarrow4x=8\Rightarrow x=2\)
6 tháng 11 2021
10.
b) \(\Leftrightarrow\left(x-3\right)\left(x-3-3+x^2\right)=0\\ \Leftrightarrow\Leftrightarrow\left(x-3\right)\left(x^2+x-6\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=-3\end{matrix}\right.\)
d) \(\Leftrightarrow x^2\left(x+5\right)-4\left(x+5\right)=0\\ \Leftrightarrow\left(x+5\right)\left(x^2-4\right)=0\\ \Leftrightarrow\left(x+5\right)\left(x-2\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-5\\x=2\\x=-2\end{matrix}\right.\)
e) \(\Leftrightarrow4x^2-4x+1-4x^2+25-18=0\\ \Leftrightarrow-4x+8=0\\ \Leftrightarrow x=2\)
22 tháng 11 2021
ĐKXĐ: \(m\ne-1,m\ne\dfrac{3}{2}\)
a) 2 đường thẳng song song
\(\Leftrightarrow\left\{{}\begin{matrix}m+1=3-2m\\n\ne-2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{2}{3}\left(tm\right)\\n\ne-2\end{matrix}\right.\)
b) 2 đường thẳng cắt nhau tại một điểm trên trục tung:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1;m\ne\dfrac{3}{2}\\m+1\ne3-2m\\n=-2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1;m\ne\dfrac{3}{2};m\ne\dfrac{2}{3}\\n=-2\end{matrix}\right.\)