Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 ,áp dụng bộ 3 pitago trong tam giác abc suy ra AC=5 cm dựa vào pitago đảo có : \(5^2+12^2\)= 13 suy ra tam giác ACD vuông tại c
S tứ giác = SABC +SADC =1/2 .3.4 +1/2. 5.12=36 cm ^2.
2,bài 2 vẽ hình lâu lém tự làm nha bn
3,
B1 minh da lam dc trc do roi nhung van cam on ban vi da giup do

 Tổng số phần của 2 diện tích tam giác :
Tổng số phần của 2 diện tích tam giác :
3 + 2 =5 ( phần )
Diện tích tam giác ACD :
70 : 5 x 3 = 52 ( cm2)
Diện tích tam giác ABC :
70 : 5 x 2 = 28 ( cm2)
Vậy : diện tích tam giác ACD : 52 cm2
______________ ABC : 28 cm2

Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân

a) Áp dụng hệ quả định lý Ta-let ta có:
ΔABC có MN // BC (M ∈ AB, N ∈ AC) ⇒ 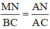
ΔAHC có KN // HC (K ∈ AH, N ∈ AC) ⇒ 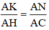
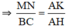
Chứng minh tương tự ta có:
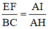
Mà ta có:
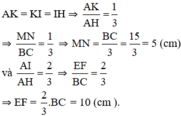
b) Ta có:


b) SABCD = \(\dfrac{1}{2}\) AH . BC
\(\Rightarrow\) 270 = \(\dfrac{1}{2}\) . AH . 15
\(\Rightarrow\) AH = \(\dfrac{270.2}{15}\) = 36 cm
Ta có AH = 3AK (câu a) và AK = KI (gt)
Do đó AH = 3KI
\(\Rightarrow\) KI = \(\dfrac{AH}{3}\) = \(\dfrac{36}{3}\) = 12 cm
SMNFE = \(\dfrac{1}{2}\) KI (MN + EF) = \(\dfrac{1}{2}\) . 12 (5 + 10) = 90 cm2
a) Ta có AH=AK+KI+IH và AK = KI = IH (gt)
\(\Rightarrow\) AH = 3AK\(\Rightarrow\) \(\dfrac{AK}{AH}\) = \(\dfrac{1}{3}\)
\(\Delta\)ABC có MK // BH (gt) \(\Rightarrow\) \(\dfrac{AM}{AB}\)= \(\dfrac{AK}{AH}\) \(\Rightarrow\) \(\dfrac{AM}{AB}\) = \(\dfrac{1}{3}\)
\(\Delta\)ABC có MN // BC (gt) \(\Rightarrow\) \(\dfrac{MN}{BC}\) = \(\dfrac{AM}{BC}\)
\(\Rightarrow\) \(\dfrac{MN}{BC}\) = \(\dfrac{1}{3}\)
\(\Rightarrow\) \(\dfrac{MN}{15}\)= \(\dfrac{1}{3}\)
\(\Rightarrow\) MN = \(\dfrac{15}{3}\) = 5 cm
...
∆AEI có MK // EI (gt) và K là trung điểm của AI (AK = KI)
\(\Rightarrow\) M là trung điểm của AE
Xét ∆AEF có MN // EF (gt)
\(\Rightarrow\) \(\dfrac{MN}{EF}\) = \(\dfrac{AM}{AE}\)
Mà \(\dfrac{AM}{AE}\) = \(\dfrac{1}{2}\) (M là trung điểm của AE)
Nên \(\dfrac{MN}{EF}\) = \(\dfrac{1}{2}\)
\(\Rightarrow\) \(\dfrac{5}{EF}\) = \(\dfrac{1}{2}\)
\(\Rightarrow\) EF = 10 cm
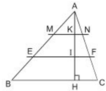
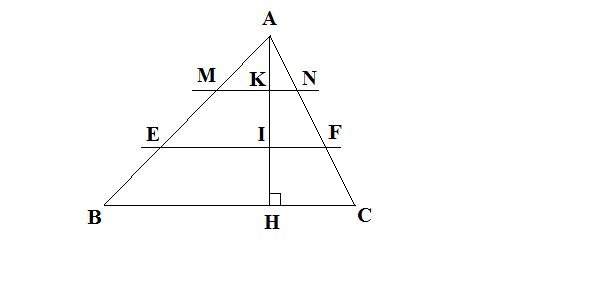 Tam giác ABC có BC = 15cm. Cho AK = KI = IH và EF // BC, MN // BC
Tam giác ABC có BC = 15cm. Cho AK = KI = IH và EF // BC, MN // BC