Cho hình thang cân ABCD có AB//CD,gọi O là giao điểm của hai đường chéo.Chứng minhOA=OA,OC=OD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


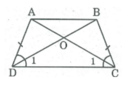
Xét ∆ ADC và ∆ BCD, ta có:
AD = BC (tính chất hình thang cân)
∠ (ADC) = ∠ (BCD) (gt)
DC chung
Do đó: ∆ ADC = ∆ BCD (c.g.c) ⇒ ∠ C 1 = ∠ D 1
Trong ∆ OCD ta có: ∠ C 1 = ∠ D 1 ⇒ ∆ OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.

a ) Xét Δ∆ADC và Δ∆BCD, ta có:
AD = BC (tính chất hình thang cân)
∠∠(ADC) = ∠∠(BCD) (gt)
DC chung
Do đó: Δ∆ADC = Δ∆BCD (c.g.c) ⇒ ∠C1∠�1= ∠D1∠�1
Trong Δ∆OCD ta có: ∠C1∠�1= ∠D1∠�1 ⇒ Δ∆OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
b)
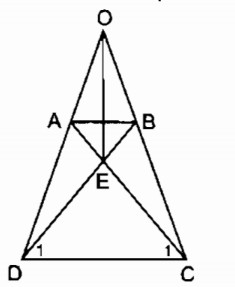
ADC=ˆBCD(gt)⇒ˆODC=ˆOCD���^=���^(��)⇒���^=���^
⇒ ∆ OCD cân tại O
⇒ OC = OD
⇒ OA + AD = OB + BC
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ∆ ADC và ∆ BCD :
AD = BC (chứng minh trên)
AC = BD (tính chất hình thang cân)
CD cạnh chung
Do đó: ∆ ADC = ∆ BCD (c.c.c)
⇒ˆD1=ˆC1⇒�^1=�^1
⇒ ∆ EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực của CD
OC = OD nên O thuộc đường trung trực của CD
E≢ O. Vậy OE là đường trung trực của CD.
BD = AC (chứng minh trên)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
E≢ O. Vậy OE là đường trung trực của AB.

Xét tam giác OAD và tam giác OBC ta có:
góc OAD = góc OCB (hai góc so le trong, AB//CD)
AD = BC (Vì hình thang cân có hai cạnh bên bằng nhau)
góc ODA = góc OBC (hai góc so le trong, AB//CD)
=> tam giác OAD = tam giac OBC (g-c-g)
=> OA=OB
chứng minh tương tự ta sẽ được OD=OC
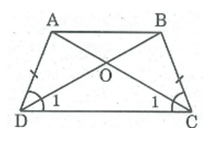
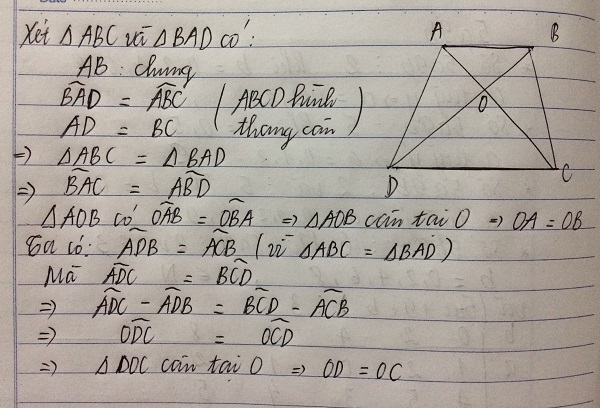
Xét \(\Delta ADC\) và \(\Delta BCD\) có:
\(AD=BC\left(gt\right)\)
\(\widehat{ADC}=\widehat{BCD}\left(gt\right)\)
Cạnh \(DC\) là cạnh chung
Vậy \(\Delta ADC=\Delta BCD\left(c.g.c\right)\)
\(\Rightarrow\widehat{C1}=\widehat{D1}\) ( 2 góc tưng ứng )
Trong \(\Delta OCB\) ta có: \(\widehat{C1}=\widehat{D1}\left(CMT\right)\)
\(\Rightarrow\Delta OCB\) cân tại \(O\)
\(\Rightarrow OC=OD\) ( cạnh tương ứng ) \(\left(1\right)\)
\(\Rightarrow AC=BD\) ( tính chất hình thang cân )
\(\Rightarrow AO+OC=BO+OD\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) suy ra \(AO=BO\)
Hình đây nhé !