cho tam giác ABC=tam giác DEF.Biết \(\widehat{A}=55^o\),\(\widehat{E}=75^o\).Tính các góc còn lại của mỗi tam giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có tam giác ABC=tam giác DEF
có góc A=55 độ;góc E=75 độ
tam giác ABC=tam giác DEF,góc A=55 độ
=>góc A=góc D=55 độ
góc E=75 độ=>góc E=góc B=75 độ
xét tam giác ABC có:A+B+C=180 độ
=>góc C=180 -(góc A+góc B)
=>góc C=50 độ
Vì tam giác ABC=tam giác DEF,góc C=50 độ
=>góc F=góc C=50 độ
vậy ....
tick nha các bạn

Vì \(\Delta ABC=\Delta DEF\) nên \(\widehat{A}\) = \(\widehat{D}\) = \(55^o\)
Ta có : \(\widehat{D}\) + \(\widehat{E}\) + \(\widehat{F}\) = \(180^o\)
\(\widehat{F}\) = \(180^o\) - \(\widehat{D}\) - \(\widehat{E}\)
\(\widehat{F}\) = \(180^o\)- \(55^o\) - \(75^o\)
\(\widehat{F}\) = \(50^o\)
Vì \(\Delta ABC=\Delta DEF\) nên \(\widehat{B}\) = \(\widehat{E}\) = \(75^o\)

Ta co goc con lai la C
Tong cac ta giax ABC la 180 do
=> A+B+C=180
=>55+75+C=180
=>75+C=180-55
=> 75+C=125
=>C = 125-75
=> C =50

Tham khảo:
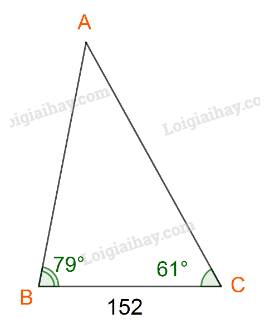
Đặt \(AB = c,AC = b,BC = a.\)
Ta có: \(a = 152;\widehat A = {180^o} - ({79^o} + {61^o}) = {40^o}\)
Áp dụng định lí sin, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Suy ra:
\(\begin{array}{l}AC = b = \frac{{a.\sin B}}{{\sin A}} = \frac{{152.\sin {{79}^o}}}{{\sin {{40}^o}}} \approx 232,13\\AB = c = \frac{{a.\sin C}}{{\sin A}} = \frac{{152.\sin {{61}^o}}}{{\sin {{40}^o}}} \approx 206,82\\R = \frac{a}{{2\sin A}} = \frac{{152}}{{2\sin {{40}^o}}} \approx 118,235\end{array}\)

\(\Delta ABC=\Delta DEF\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=\widehat{D}=55^0\\\widehat{E}=\widehat{B}=75^0\end{matrix}\right.\\ \Rightarrow\widehat{C}=\widehat{F}=180^0-\widehat{A}-\widehat{B}=50^0\)

Ta có: tam giác ABC = tam giác DEF.
=> góc A = góc D = 55 độ
góc B = góc E = 75 độ
góc C = góc F
Trong tam giác ABC ta có:
góc A + góc B + góc C = 180* (tổng 3 góc của tam giác)
55* + 75* + góc C = 180*
góc C = 180* - (55*+75*)
góc C = 180* - 130* = 50*
Vậy góc A = góc D = 55 độ
góc B = góc E = 75 độ
góc C = góc F = 50*
Ta có tam giác ABC= tam giác DEF Có góc A = 55 độ ; Góc E =75 độ => Góc A = 55 độ , D = 55 độ => Góc E = 75 độ ; Góc B = 75 độ Xét tam giác ABC có : A+B+C=180 độ =>góc C= 180 - (Góc A+ góc B) =>gócC=180- 130= 50 độ
=> góc C = 50 độ

Áp dụng định lí cosin trong tam giác ABC
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\quad (1)\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\quad (2)\end{array}\)
(trong đó: AB = c, BC = a và AC = b)
Ta được: \(B{C^2} = {a^2} = {8^2} + {5^2} - 2.8.5.\cos {45^o} = 89 - 40\sqrt 2 \)\( \Rightarrow BC \approx 5,7\)
Từ (2) suy ra \(\cos B = \frac{{{a^2} + {c^2} - {b^2}\,}}{{2a\,c}}\);
Mà: a = BC =5,7; b =AC = 8; c =AB =5.
\( \Rightarrow \cos B \approx \frac{{ - 217}}{{1900}} \Rightarrow \widehat B \approx {97^o} \Rightarrow \widehat C \approx {38^o}\)
Vậy tam giác ABC có BC = 5,7, \(\widehat B = {97^o},\widehat C = {38^o}\)

à làm thêm câu b):
Vì \(\Delta\text{ABC}=\Delta\text{MNP}\)nên:
AB=MN=5cm; AC=MP=7cm và BC=NP.
Trong tam giác ABC có:
AB+BC+CA=22 (cm)
=> 5 + BC + 7 = 22
=> BC = 22 - 5 - 7
=> BC = 10 (cm)
Mà BC = NP = 10 cm
Vậy...(bạn viết tương tự nhé).
trời ạ
ta có tam giác ABC= tam giác DEF
suy ra góc A = góc D , góc b = góc E , góc C = góc F
trong tam giác ABC CÓ góc A + góc B +góc C = 180 độ
mà góc A=55 độ , B = 75 độ
suy ra góc C =50 độ
mà góc C = góc F = 50 độ
góc D = góc A =55 độ
góc B = góc E = 75 độ
cho mình nha
thanhks
giải
Ta có : \(\Delta ABC=\Delta DEF\)
\(\Rightarrow\widehat{A}=\widehat{D}=55^0\)
\(\widehat{B}=\widehat{E}=75^0\)
Ta có tổng 3 góc trong một tam giác bằng 1800
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=\widehat{D}+\widehat{E}+\widehat{F}=180^0\)
\(\Rightarrow\widehat{C}=180^0-\left(\widehat{A}+\widehat{B}\right)=180^0-\left(55^0+75^0\right)\)
\(\Rightarrow\widehat{C}=\widehat{F}=50^0\)