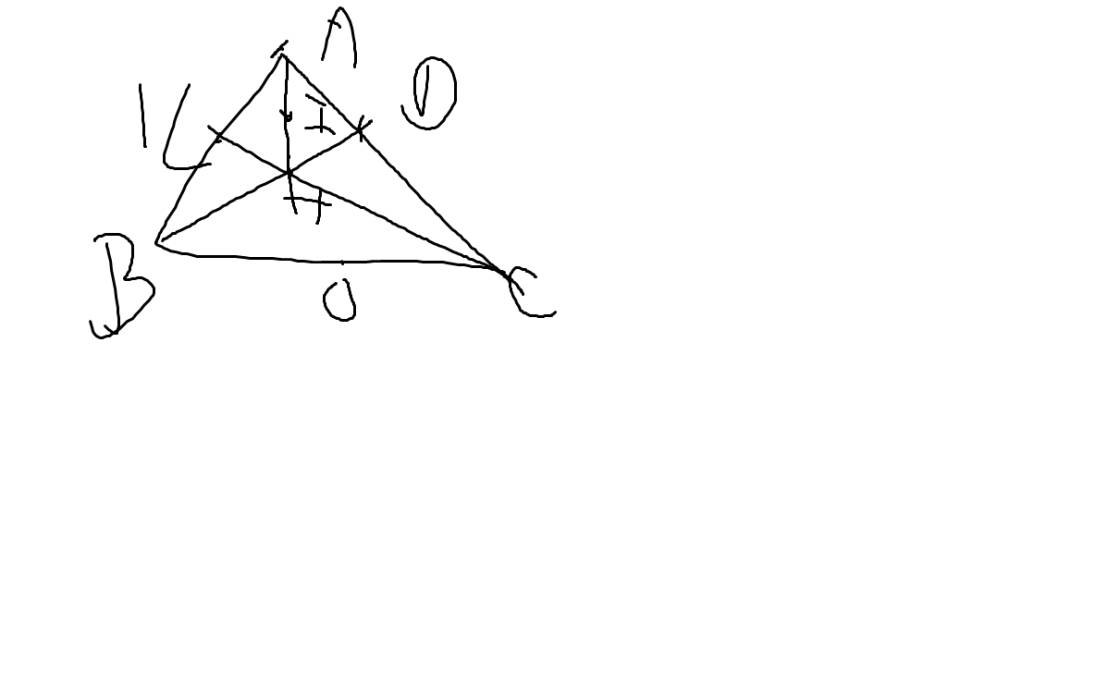
Cho tam giác ABC nhọn. Đường cao BD, CK cắt nhau tại H
a. Cm 4 điểm B, D, C, K thuộc đường tròn
b. So sánh BC và DK
c. Cm 4 điểm A, D, H, K cùng thuộc 1 đường tròn
d. Gọi I là tâm của đường tròn . Cm IK vuông góc KO (O là trung điểm BC)
Vẽ hình giúp mình là được rồi ạa