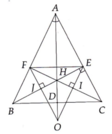
4.Cho tam giác abc nhọn có 3 đường cao AD,BE,CF. qua A kẻ a//BC. Qua B kẻ b//CA. Qua C kẻ c//AB. gọi MNP là tam giác được tạo bởi 3 đường thẳng a b c. chứng mibh AD,BE,CD là 3 đường trung trực của MNP em cần gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 4 2023
a: Kẻ AN là đường kính của (O)
góc ABN=1/2*180=90 độ
=>BN//CH
góc ACN=1/2*180=90 độ
=>CH//BN
=>BHCN là hình bình hành
=>M là trung điểm của HN
Xét ΔAHN có NM/NH=NO/NA
nên OM//AH và OM=AH/2
=>AH=2OM
c: ΔOKL cân tại O
mà OI là đường cao
nên I là trung điểm của KL
13 tháng 10 2023
Sửa đề: Từ C,B kẻ các đường thẳng vuông góc với AC,AB cắt nhau tại K
a: CK vuông góc AC
BH vuông góc AC
Do đó: CK//BH
BK vuông góc AB
CH vuông góc AB
Do đó: BK//CH
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành
b: BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
=>H,M,K thẳng hàng
6 tháng 1
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=15^2-9^2=144\)
=>\(AC=\sqrt{144}=12\left(cm\right)\)
b: Xét ΔCAB vuông tại A và ΔCDE vuông tại D có
CA=CD
\(\widehat{ACB}=\widehat{DCE}\)(hai góc đối đỉnh)
Do đó: ΔCAB=ΔCDE
=>CB=CE
=>C là trung điểm của BE
Xét ΔFBE có
FC là đường cao
FC là đường trung tuyến
Do đó: ΔFBE cân tại F
Xét tứ giác ABCN có
AB//CN
AN//BC
Do đó: ABCN là hbh
=>AN=BC và AB=CN
Xét tứ giác AMBC có
AM//BC
BM//AC
Do đó: AMBC là hình bình hành
=>BM=AC và AM=BC
Xét tứ giác ABPC có
AB//PC
AC//BP
Do đó: ABPC là hình bình hành
=>AB=CP và AC=BP
AC=BP
AC=BM
Do đó: BP=BM
=>B là trung điểm của PM
AM=BC
AN=BC
Do đó: AM=AN
=>A là trung điểm của MN
AB=CN
AB=CP
=>CN=CP
=>C là trung điểm của NP
BE vuông góc AC
AC//MP
Do đó: BE vuông góc MP
=>EB là đường trung trực của MP
CF vuông góc AB
AB//NP
Do đó: FC vuông góc NP
mà C là trug điểm của NP
nên FC là trung trực cuả NP
AD vuông góc BC
BC//MN
Do đó: DA vuông góc MN
mà A là trung điểm của MN
nên DA là trung trực của MN