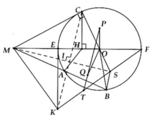
Cho góc nhọn xOy vầ điểm M nằm ở miền trong của góc nhọn. Gọi E và F lần lượt là hình chiếu của M trên Ox và Oy. Vẽ các đường tròn đường kính ME và MF cắt OM lần lượt tại P,Q; EF cắt OM tại H . CMR:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: M nằm trên tia phân giác của góc xOy
Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
góc AOM=góc BOM
=>ΔOAM=ΔOBM
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>O,C,P thẳng hàng và OP vuông góc với AB tại P
=>CP là trung trực của ΔCAB

a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
=>MA=MB
Xét ΔMAF vuông tại A và ΔMBE vuông tại B có
MA=MB
\(\widehat{AMF}=\widehat{BME}\)
Do đó: ΔMAF=ΔMBE
=>MF=ME
b:
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(1)
Ta có: MA=MB
=>M nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra OM là đường trung trực của BA
=>OM\(\perp\)BA

a, HS tự chứng minh
b, MH.MO = MA.MB ( = M C 2 )
=> ∆MAH:∆MOB (c.g.c)
=> M H A ^ = M B O ^
M B O ^ + A H O ^ = M H A ^ + A H O ^ = 180 0
=> AHOB nội tiếp
c, M K 2 = ME.MF = M C 2 Þ MK = MC
∆MKS = ∆MCS (ch-cgv) => SK = SC
=> MS là đường trung trực của KC
=> MS ^ KC tại trung của CK
d, Gọi MS ∩ KC = I
MI.MS = ME.MF = M C 2 => EISF nội tiếp đường tròn tâm P Þ PI = PS. (1)
MI.MS = MA.MB (= M C 2 ) => AISB nội tiếp đường tròn tâm Q Þ QI = QS. (2)
Mà IT = TS = TK (do DIKS vuông tại I). (3)
Từ (1), (2) và (3) => P, T, Q thuộc đường trung trực của IS => P, T, Q thẳng hàng
Để chứng minh QO⋅QMOP⋅PM=HF^2/HE^2, ta sẽ sử dụng định lí hình học và tính chất của các tam giác đồng dạng.
Đầu tiên, ta cần chứng minh tam giác QOM và tam giác MOP đồng dạng. Ta có:
∠QOM = ∠MOP (do chúng là góc đối) ∠OQM = ∠OMP (do chúng là góc ở chung) => Tam giác QOM đồng dạng với tam giác MOP theo định lí góc-góc (AA).
Từ đó, ta có tỷ lệ giữa các cạnh của hai tam giác này:
QM/OP = OQ/OM (tỷ lệ cạnh tương ứng của hai tam giác đồng dạng) => QM = OQ/OM * OP
Tiếp theo, ta cần chứng minh tam giác HEF và tam giác HOM đồng dạng. Ta có:
∠HEF = ∠HOM (do chúng là góc đối) ∠EHF = ∠OHM (do chúng là góc ở chung) => Tam giác HEF đồng dạng với tam giác HOM theo định lí góc-góc (AA).
Từ đó, ta có tỷ lệ giữa các cạnh của hai tam giác này:
HE/OM = EF/OM (tỷ lệ cạnh tương ứng của hai tam giác đồng dạng) => HE = EF/OM * OM => HE = EF
Như vậy, ta có HE = EF.
Bây giờ, ta sẽ xem xét tỷ lệ giữa các đoạn thẳng QO, QM, OP, PM và HF, HE:
QO⋅QMOP⋅PM = (OQ/OM * OP) * (OP) * (PM) = OQ * OP * PM / OM = OQ * PM
Vì HE = EF, nên ta có:
HF/HE = QM/OM (tỷ lệ cạnh tương ứng của hai tam giác đồng dạng HEF và HOM) => HF = QM/OM * HE
Thay giá trị của HE = EF vào, ta có:
HF = QM/OM * EF
Vậy, ta thấy HF^2 = (QM/OM * EF)^2
Như vậy, ta có:
QO⋅QMOP⋅PM = HF^2/HE^2
Vậy, điều phải chứng minh đã được chứng minh.