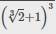mn giải chi tiết giúp mình bước tách ra được ko ạ tại mình ko hiểu cách tách lắm. cảm ơn mn !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KT
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
1
14 tháng 10 2021
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
LH
1
10 tháng 10 2020
E = 2x2 + 3x + 8
= 2( x2 + 3/2x + 9/16 ) + 55/8
= 2( x + 3/4 )2 + 55/8 ≥ 55/8 ∀ x
Dấu "=" xảy ra khi x = -3/4
=> MinE = 55/8 <=> x = -3/4
19 tháng 2 2022
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
NC
2
9 tháng 11 2021
Bài 1:
\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)
Bài 2:
\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)
9 tháng 11 2021
Bài 3:
\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)
Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)
Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)
Bài 4:
\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)
GB
1
15 tháng 4 2022
\(∘ backwin\)
\(CD:1 × 4 = 4 ( c m )\)
\(CR:1 × 3 = 3 ( c m )\)
\(Chiều\) \(cao:1 × 4 = 4 ( c m )\)
\(V: 4 × 3 × 4 = 48 ( c m ^3 )\)
\(Đ/s:48cm^3\)
DH
1
HT
6 tháng 1 2021
Okie, xinh nên giúp :3 Đùa thui
a/ 5 nguồn mắc nối tiếp \(\left\{{}\begin{matrix}\xi_b=5.\xi=5.4=20\left(V\right)\\r_b=5r=5.0,2=1\left(\Omega\right)\end{matrix}\right.\)
b/ \(R_D=\dfrac{U^2_{dm}}{P_{dm}}=\dfrac{36}{6}=6\left(\Omega\right);I_{dm}=\dfrac{P_{dm}}{U_{dm}}=\dfrac{6}{6}=1\left(A\right)\)
Đèn sáng bình thường \(\Rightarrow I_2=I_D=I_{dm}=1\left(A\right)\)
\(\left(R_1ntR_B\right)//\left(R_2ntR_D\right)\Rightarrow R_{td}=\dfrac{\left(R_1+R_B\right)\left(R_2+R_D\right)}{R_1+R_B+R_2+R_D}=\dfrac{\left(2+4\right)\left(6+6\right)}{2+4+6+6}=4\left(\Omega\right)\)
c/ \(I=\dfrac{\xi_b}{r_b+R_{td}}=\dfrac{20}{1+4}=4\left(A\right)\)
\(I=I_1+I_2\Rightarrow I_1=I-I_2=4-1=3\left(A\right)\Rightarrow P_1=I_1^2.R_1=3^2.2=18\left(W\right)\)
\(m_{Cu}=\dfrac{A_{Cu}.I_B.t}{F.n}=\dfrac{64.3.\left(32.60+10\right)}{96500.2}=...\left(g\right)\)
92
1
11 tháng 7 2023
a: Khi m=2 thì (1) sẽ là:
2x+y=2 và 4x+3y=10
=>x=-2 và y=6
b: 2x+y=m và 4x+3y=10
=>4x+2y=2m và 4x+3y=10
=>4x+3y=10 và 4x+2y=2m
=>y=10-2m và 2x=m-10+2m=3m-10
=>y=10-2m và x=3/2m-5
x>0 và y>0
=>10-2m>0 và 3/2m-5>0
=>m>5:3/2=10/3 và m<5
=>10/3<m<5
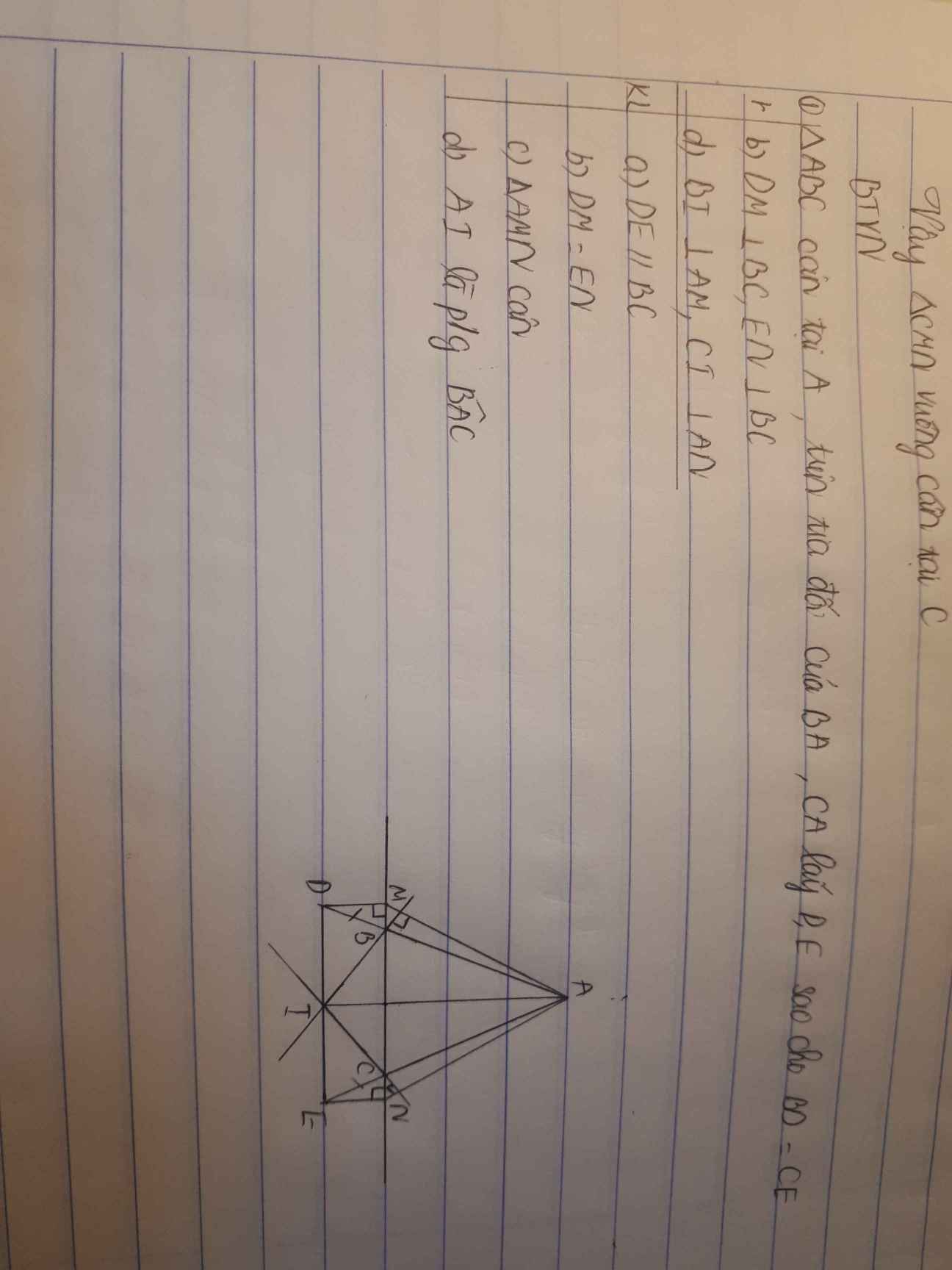
giúp mình với