mọi người giải giúp e với ạ

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hmm, nói đến cờ chắc là dấu hiệu của semaphore, thử mò xem :v

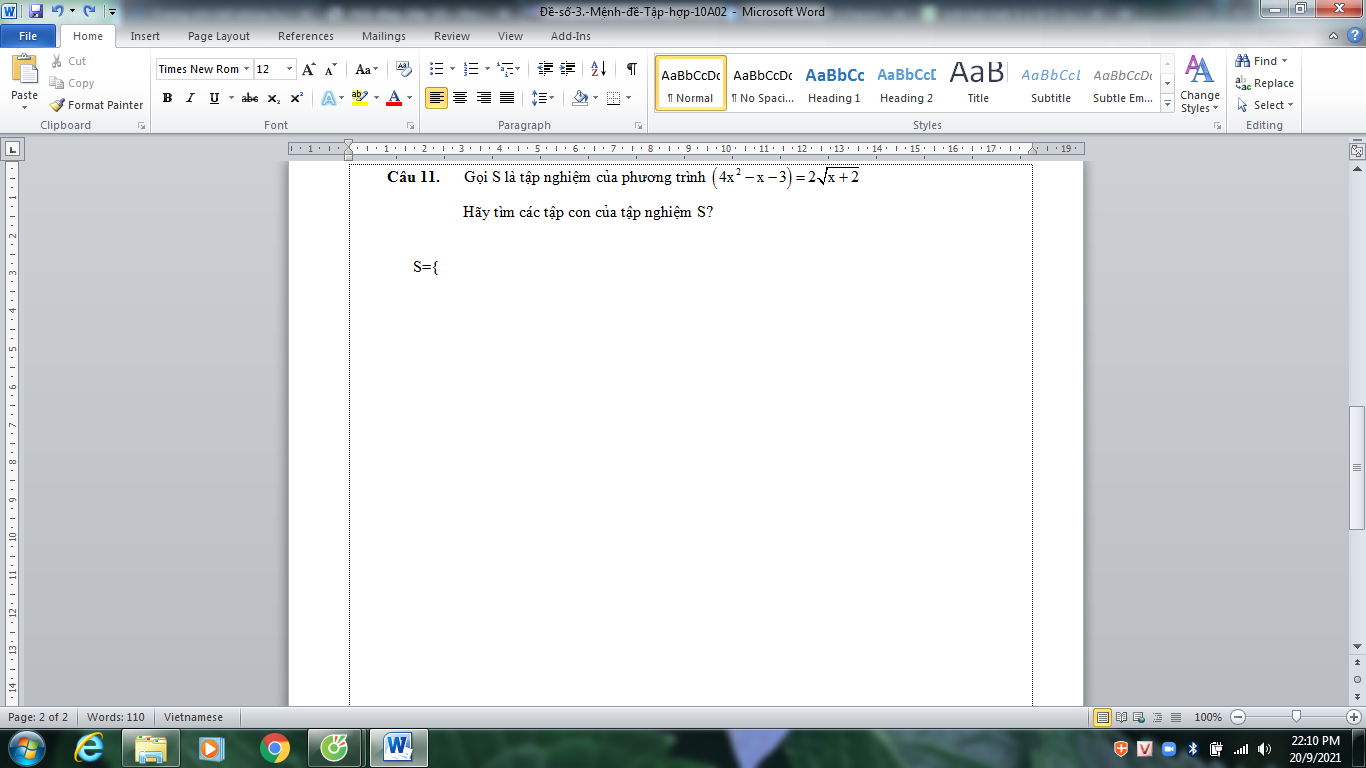
\(\Leftrightarrow4x^2=x+2+2\sqrt{x+2}+1\)
\(\Leftrightarrow\left(\sqrt{x+2}+1\right)^2=\left(2x\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x+2}+1=2x\\\sqrt{x+2}+1=-2x\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x+2}=2x-1\left(x\ge\dfrac{1}{2}\right)\\\sqrt{x+2}=-2x-1\left(x\le-\dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+2=4x^2-4x+1\left(x\ge\dfrac{1}{2}\right)\\x+2=4x^2+4x+1\left(x\le-\dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{41}}{8}\\x=-1\end{matrix}\right.\)


Lời giải:
$\frac{x-2y}{3z}$ có thể nhận giá trị lớn nhất nếu $x$ lớn nhất và $y,z$ nhỏ nhất có thể.
$x$ lớn nhất có thể nhận là $14$ (theo điều kiện)
$y,z$ nhỏ nhất có thể nhận là $1,2$ (do $y,z$ phân biệt)
Nếu $x=14, y=1,z=2$ thì $\frac{x-2y}{3z}=2$
Nếu $x=14; y=2, z=1$ thì $\frac{x-2y}{3z}=\frac{10}{3}>2$
Đáp án D.


24: Ta có: \(A=10ax-5ay+2x-y\)
\(=5a\left(2x-y\right)+\left(2x-y\right)\)
\(=\left(2x-y\right)\left(5a+1\right)\)
25: Ta có: \(A=10ax-5ay-2x+y\)
\(=5a\left(2x-y\right)-\left(2x-y\right)\)
\(=\left(2x-y\right)\left(5a-1\right)\)

Câu 1:
Gọi chiều rộng là x
Chiều dài là x+20
Theo đề, ta có: 2(x+x+20)=104
=>2x+20=52
=>2x=32
hay x=16
Vậy: Diện tích của miếng đất là 16x36=576(m2)
Xin lỗi nhưng e cần bài này dạng Giải bài bằng cách lập hệ phương trình ạ





Bạn cảm ơn ai thế
cũng ko bt