Xác định đường thẳng (d) đi qua điểm A(1;7) và có hệ số góc bằng 1....
Đọc tiếp
Xác định đường thẳng (d) đi qua điểm A(1;7) và có hệ số góc bằng 1.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 6 2023
2:
a: Hệ số góc là 5 nên -2m+1=5
=>-2m=4
=>m=-2
b: (d1)//(d)
=>-2m+1=3 và m+3<>7
=>m=-1
c: Hai đường vuông góc với nhau
=>-1/2(-2m+1)=-1
=>m^2-1/2+1=0
=>m^2+1/2=0(loại)
CM
5 tháng 11 2018
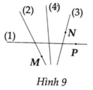
-Đường thẳng a là đường thẳng số 2
-Đường thẳng b là đường thẳng số 1
-Đường thẳng c là đường thẳng số 3
-Đường thẳng d là đường thẳng số 4
5 tháng 7 2021
a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
Vậy: (d): y=2x+b
Vì (d) đi qua điểm C(-1;4) nên
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
hay b=6
Vậy: (d): y=2x+6
Thay y=0 vào (d), ta được:
2x+6=0
hay x=-3
Vậy: A(-3;0)
b) Vì y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\b=a+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=\dfrac{-4}{5}+4=\dfrac{-4}{5}+\dfrac{20}{5}=\dfrac{16}{5}\end{matrix}\right.\)
4 tháng 7 2021
a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên ta có: \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
=> (d): y=2x+b
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
\(\Leftrightarrow b=6\)
Vậy: (D): y=2x+6
Thay y=0 vào (d),ta được:
\(2x+6=0\)
\(\Leftrightarrow x=-3\)
Vậy: A(-3;0)
b) Vì đồ thị hàm số y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\-a+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=4+a=4+\dfrac{-4}{5}=4-\dfrac{4}{5}=\dfrac{16}{5}\end{matrix}\right.\)
Vậy: \(a=-\dfrac{4}{5}\); \(b=\dfrac{16}{5}\)
c) Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(-3-4\right)^2+\left(0-0\right)^2}=7\)(cm)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(-3+1\right)^2+\left(0-4\right)^2}=2\sqrt{5}\left(cm\right)\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(4+1\right)^2+\left(0-4\right)^2}=\sqrt{41}\left(cm\right)\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC\)
\(=7+2\sqrt{5}+\sqrt{41}\)
\(\simeq17,9\left(cm\right)\)
5 tháng 7 2021
Còn thiếu tính góc tạo bởi đường thẳng BC và trục Ox mà bạn
18 tháng 12 2021
a: Thay x=1 và y=-1 vào (d), ta được:
m+1=-1
hay m=-2
18 tháng 11 2021
\(a,\Leftrightarrow\left\{{}\begin{matrix}a=3;b\ne1\\2a+b=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-1\end{matrix}\right.\\ b,\Leftrightarrow\left\{{}\begin{matrix}a=1;b\ne-5\\B\left(-2;0\right)\inđths\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1;b\ne-5\\-2a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\\ c,\Leftrightarrow\left\{{}\begin{matrix}-a+b=2\\2a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{3}\\b=\dfrac{1}{3}\end{matrix}\right.\)
20 tháng 9 2021
\(a,\) Gọi pt đường thẳng \(\left(d\right)\) là \(y=ax+b\)
Ta có \(\left(d\right)\) đi qua \(A\left(-3;0\right),B\left(0;2\right)\) nên \(\left\{{}\begin{matrix}0=-3a+b\\2=0a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{2}{3}\\b=2\end{matrix}\right.\)
Vậy đths là \(\left(d\right):y=\dfrac{2}{3}x+2\)
\(b,\) Gọi pt đường thẳng \(\left(d\right)\) là \(y=ax+b\)
Ta có hệ pt \(\left\{{}\begin{matrix}1=0a+b\\0=-a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)
Vậy đths là \(\left(d\right):y=x+1\)
20 tháng 9 2021
a,a, Gọi pt đường thẳng (d)(d) là y=ax+by=ax+b
Ta có (d)(d) đi qua A(−3;0),B(0;2)A(−3;0),B(0;2) nên {0=−3a+b2=0a+b⇔⎧⎨⎩a=23b=2{0=−3a+b2=0a+b⇔{a=23b=2
Vậy đths là (d):y=23x+2(d):y=23x+2
b,b, Gọi pt đường thẳng (d)(d) là y=ax+by=ax+b
Ta có hệ pt {
Lời giải:
Gọi ptđt $(d)$ có hệ số góc bằng $1$ là $y=x+b$
Vì $(d)$ đi qua $A(1,7)$ nên:
$y_A=x_A+b$
$\Leftrightarrow 7=1+b$
$\Leftrightarrow b=6$
Vậy ptđt $(d)$ cần tìm là $y=x+6$