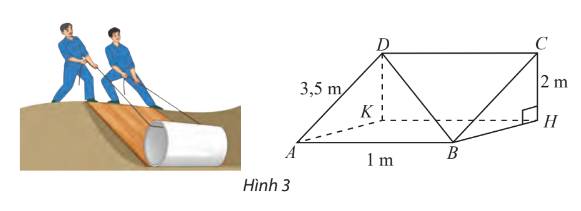
Một tấm ván hình chữ nhật \(ABCD\) được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu 2 m. Cho biết \(AB = 1\,m,AD = 3,5{\rm{ }}m\). Tính góc giữa đường thẳng \(BD\) và đáy hồ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

P.h = F.s
225.2 = 1,8F
450 = 1,8F
=> F = 450 : 1,8 = 250N
Vậy khi tấm ván dài 1,8m Bình phải dùng 1 lực kéo vật là 250N

P=10m=50.10=500N
công đưa vật lên cao 1m:
A=P.h=500.1=500(J)
Áp dụng định luật bảo toàn công ta có: công kéo vật bằng MPN=công kéo vật trực tiếp
Lực kéo lên dùng MPN:
F=A/S=500/2=250(N)

Bài 6 :
\(A_{cóich}=P.h=600.0,8=480\left(J\right)\)
\(A_{tp}=F.s=300.2,5=750\left(J\right)\)
\(H=\dfrac{A_{ci}}{A_{tp}}=64\%\)
Bài 7 :
a/ Ko có ma sát \(\Leftrightarrow F.l=P.h\Leftrightarrow l=\dfrac{P.h}{F}=8\left(m\right)\)
b/ Có ma sát :
\(A_{ci}=P.h=1000\left(J\right)\)
\(A_{tp}=F.l=1200\left(J\right)\)
\(H=\dfrac{A_{ci}}{A_{tp}}=83,33\%\)

Ta thấy lực kéo trên mặt phẳng nghiêng và độ dài mặt phẳng nghiêng tỉ lệ nghịch với nhau hay:
l1/l2=F2/F1=>F2=F1.l1/l2=250N
vật bình phải dùng lực kéo là 250N

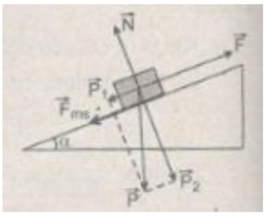
Chọn chiều chuyển động của vật m là chiều dương. Phương trình của định luật II Niu-tơn đối với vật m chuyển động trên mặt phẳng nghiêng như hình vẽ có dạng:
ma = F – P 1 - F m s
Với P 1 = mg.sin 30 ° ≈ 400 N.
F m s = μN = µmgcos 30 ° ≈ 13,8 N.
Khi vật chuyển động thẳng đều: a = 0, lực kéo có độ lớn:
F = P 1 + F m s ≈ 413,8 N
Do đó, công của lực kéo: A = Fs = 413,8.2,5 = 1034,5 J.

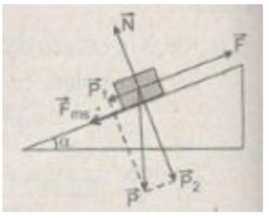
Chọn chiều chuyển động của vật m là chiều dương. Phương trình của định luật II Niu-tơn đối với vật m chuyển động trên mặt phẳng nghiêng như hình vẽ có dạng:
ma = F – P 1 - F m s
Với P 1 = mg.sin 30 ° ≈ 400 N.
F m s = μN = µmgcos 30 ° ≈ 13,8 N.
Khi vật chuyển động với gia tốc a = 1,5 m/ s 2 , lực kéo có độ lớn:
F = P 1 + F m s + ma ≈ 413,8 + 80.1,5 = 533,3 N
Công của lực kéo: A = Fs = 533,8.2,5 = 1334,5 J

Tóm tắt
\(s=8m\)
\(m=50kg\)
\(\Rightarrow P=10.m=10.50=500N\)
\(h=3,5m\)
\(F_{cms}=700N\)
_____________________
\(F_{ms}=?\)
Công của người đó khi kéo vật lên cao 3,5 m là:
\(A=P.h=500.3,5=1750\left(J\right)\)
Lực kéo của người đó trên mặt phẳng nghiêng khi không có ma sát là:
\(A=F_{kms}.s\Rightarrow F_{kms}=\dfrac{A}{s}=\dfrac{1750}{8}=218,75\left(N\right)\)
Lực ma sát giữa vật và mặt phẳng nghiêng là:
\(F_{ms}=F_{cms}-F_{kms}=700-218,75=481,25\left(N\right)\)
Tóm tắt:
\(m=50kg\Rightarrow P=10m=500N\)
\(s=8m\)
\(h=3,5m\)
\(F=700N\)
==========
\(F_{ms}=?N\)
Công có ích thực hiện được:
\(A_i=P.h=500.3,5=1750J\)
Công toàn phần thực hiện được:
\(A_{tp}=F.s=700.8=5600J\)
Công của lực ma sát:
\(A_{ms}=A_{tp}-A_i=5600-1750=3850J\)
Độ lớn của lực ma sát:
\(A_{ms}=F_{ms}.s\Rightarrow F_{ms}=\dfrac{A_{ms}}{s}=\dfrac{3850}{8}=481,25N\)
\(DK \bot \left( {ABHK} \right) \Rightarrow \left( {B{\rm{D}},\left( {ABHK} \right)} \right) = \left( {B{\rm{D}},BK} \right) = \widehat {DBK}\)
\(DK = CH = 2,AK = \sqrt {A{{\rm{D}}^2} - D{K^2}} = \frac{{\sqrt {33} }}{2},KB = \sqrt {A{K^2} + A{B^2}} = \frac{{\sqrt {37} }}{2}\)
\(\tan \widehat {DBK} = \frac{{DK}}{{KB}} = \frac{4}{{\sqrt {37} }} \Rightarrow \widehat {DBK} \approx 33,{3^ \circ }\)
Vậy góc giữa đường thẳng \(BD\) và đáy hồ bằng \(33,{3^ \circ }\).