Cho tứ giác ABCD. Y, J theo thứ tự là trung điểm của AC và BD.
C/m: AC+BD+2YJ < AB+BC+CD+AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 11 2015
Ta co:IA =IB(gt) ; HA =HC(gt)
Suy ra:HI la` đg tb của tam giac ABC
Suy ra:IH =1/2BC ;IH//BC (1)
Trong tam giac BDC co:KD =KB(gt) ;JD =JC(gt)
Suy ra :KJ la đg tb cu`a tam giac BDC
Suy ra :KJ =1/2BC ;KJ//BC (2)
Tu (1) va (2) suy ra :KJ = IH ;KJ // IH
Suy ra :tu giac KIHJ la hinh binh hanh(2 canh doi song song va bang nhau)(*)
Trong tam giac ADC co:HA =HC(gt) ;JD = JC(gt)
Suy ra :HJ la đg tb của tam giac ADC
Suy ra :HJ = 1/2AD
Mà AD =BC(gt) ; HI = 1/2BC(c/m tren)
Suy ra :HJ = HI (**)
Tu (*) va (**) suy ra tu giac KIHJ la hinh thoi (hbh co 2 canh ke bang nhau)
Suy ra :IJ vuong goc voi KH
CM
17 tháng 12 2017
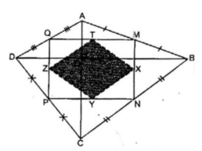
Kẻ đường chéo MP và NQ
Trong △ MNP ta có:
X là trung điểm của MN
Y là trung điểm của NP
nên XY là đường trung bình của △ MNP
⇒ XY // MP và XY = 1/2 MP (tính chất đường trung bình của tam giác) (3)
Trong △ QMP ta có:
T là trung điểm của QM
Z là trung điểm của QP
nên TZ là đường trung bình của △ QMP
⇒ TZ // MP và TZ = 1/2 MP (tính chất đường trung bình của tam giác) (4)
Từ (3) và (4) suy ra: XY // TZ và XY = TZ nên tứ giác XYZT là hình bình hành.
Trong △ MNQ ta có XT là đường trung bình
⇒ XT = 1/2 QN (tính chất đường trung bình của tam giác)
Tứ giác MNPQ là hình chữ nhật ⇒ MP = NQ
Suy ra: XT = XY. Vậy tứ giác XYZT là hình thoi
S X Y Z T = 1/2 XZ. TY
mà XZ = MQ = 1/2 BD = 1/2. 8 = 4 (cm);
TY = MN = 1/2 AC = 1/2 .6 =3 (cm)
Vậy : S X Y Z T = 1/2. 3. 4 = 6( c m 2 )
CM
21 tháng 1 2019
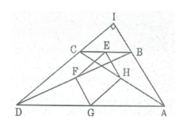
* Trong ∆ BCD, ta có:
E là trung điểm của BC (gt)
F là trung điểm của BD (gt)
Suy ra EF là đường trung bình của ∆ BCD
⇒ EF // CD và EF = 1/2 CD (1)
* Trong ∆ ACD, ta có: H là trung điểm của AC (gt)
G là trung điểm của AD (gt)
Suy ra HG là đường trung bình của ∆ ACD
⇒HG // CD và HG = 1/2 CD (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
* Mặt khác: EF // CD (chứng minh trên)
AB ⊥ CD (gt)
Suy ra EF ⊥ AB
Trong ∆ ABC ta có HE là đường trung bình ⇒ HE // AB
Suy ra: HE ⊥ EF hay ∠ (FEH) = 90 0
Vậy hình bình hành EFGH là hình chữ nhật.
17 tháng 8 2016
Áp dụng tính chất đường trung bình vào các tam giác ABD, BDC, ABC, ADC ta chứng minh được
\(MI=MJ=JN=NI=\frac{AD}{2}=\frac{BC}{2}\)
=> Tứ giác MINJ là hình thoi.
Xét ▲ODC ta có:
\(\widehat{ADC}+\widehat{DCB}=90^o\)
\(\Rightarrow\widehat{COD}=90^o\)
Có: \(\widehat{MIN}=\widehat{COD}=90^o\) (cạnh tương ứng song song)
\(\Rightarrow MINJ\) là hình thoi vuông.
26 tháng 10 2018
Xét Tam giác ABC có: N là trung điểm AC, P là trung điểm của AB
=> PM là đường trung bình của tam giác ABC=> PM//=1/2BC
Tương tự: NQ//=1/2 BC
PN//=1/2 AD
MQ//=1/2AD
Mà BC=AD => PM=NQ=PN=MQ=> Tứ giác MPNQ là hình thoi=> MN vuông góc PQ
9 tháng 9 2023
Sửa đề; EG=FH
Xét ΔABD có
E,H lần lượt là trung điểm của AB,AD
=>EH là đường trung bình
=>EH//BD và EH=BD/2(1)
Xét ΔCBD có
F,G lần lượt là trung điểm của CG,CD
=>FG là đường trung bình
=>FG//BD và FG=BD/2(2)
Từ (1), (2) suy ra EH//FG và EH=FG
Xét tứ giác EHGF có
EH//FG
EH=FG
=>EHGF là hình bình hành
mà EG=FH
nên EHGF là hình chữ nhật
=>EH vuông góc HG
mà EH//BD
nên BD vuông góc HG
mà HG//AC
nên AC vuông góc BD