Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BC ( 4,5 ) = { 20,40,60...}
=> x - 5 = { 20,40,60,....}
=> x = { 25,45,....}
vậy không có giá trị x thỏa mãn điều kiện đề bài
đúng
thì
cho
xin
1
nhé
BC(4,5) = 4 . 5 = 20
-> x - 5 = 20
=> x - 5 = 20
x = 20 + 5
x = 25
\(\Rightarrow\)Vậy : x = 25
\(\rightarrow x\in\Phi\)
Bài 3: \(A=\frac{\left(2a+b+c\right)\left(a+2b+c\right)\left(a+b+2c\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
Đặt a+b=x;b+c=y;c+a=z
\(A=\frac{\left(x+y\right)\left(y+z\right)\left(z+x\right)}{xyz}\ge\frac{2\sqrt{xy}.2\sqrt{yz}.2\sqrt{zx}}{xyz}=\frac{8xyz}{xyz}=8\)
Dấu = xảy ra khi \(a=b=c=\frac{1}{3}\)
Bài 4: \(A=\frac{9x}{2-x}+\frac{2}{x}=\frac{9x-18}{2-x}+\frac{18}{2-x}+\frac{2}{x}\ge-9+\frac{\left(\sqrt{18}+\sqrt{2}\right)^2}{2-x+x}=-9+\frac{32}{2}=7\)
Dấu = xảy ra khi\(\frac{\sqrt{18}}{2-x}=\frac{\sqrt{2}}{x}\Rightarrow x=\frac{1}{2}\)
\(\left(x+1\right)\left(x-2\right)< 0\) <=> x+1 và x-2 khác dấu
Mà x+1 > x-2
=>\(x+1>0\) và \(x-2< 0\)
=>\(x>-1\) và \(x< 2=>-1< x< 2=>x\in\left\{0;1\right\}\)
Vậy....................
\(a,\left(x+1\right)\left(x-2\right)< 0\)
\(\Rightarrow\hept{\begin{cases}x+1>0\\x-2< 0\end{cases}\Rightarrow\hept{\begin{cases}x>-1\\x< 2\end{cases}\Rightarrow}-1< x< 2\left(tm\right)}\)
\(\Rightarrow\hept{\begin{cases}x+1< 0\\x-2>0\end{cases}\Rightarrow\hept{\begin{cases}x< -1\\x>2\end{cases}\Rightarrow}2< x< -1\left(KTM\right)}\)
a)=>x+1<0=>x<-1
x-2 =<0=> x=<2
b)x-2>0=>x>2
x+2/3>=0=>x>=-2/3
đặt A=\(\left(x^2-1\right)\left(x^2-4\right)\left(x^2-7\right)\left(x^2-10\right)\) âm mà \(x^2-1>x^2-4>x^2-7>x^2-10\)
=>\(x^2-10\) âm
hoặc \(x^2-10,x^2-7\) và \(x^2-4\) âm
nếu \(x^2-10\) mà \(x^2-7\) dương
=>x=3
tương tự 3 số âm thì x=2
Vậy x=2 hoặc 3
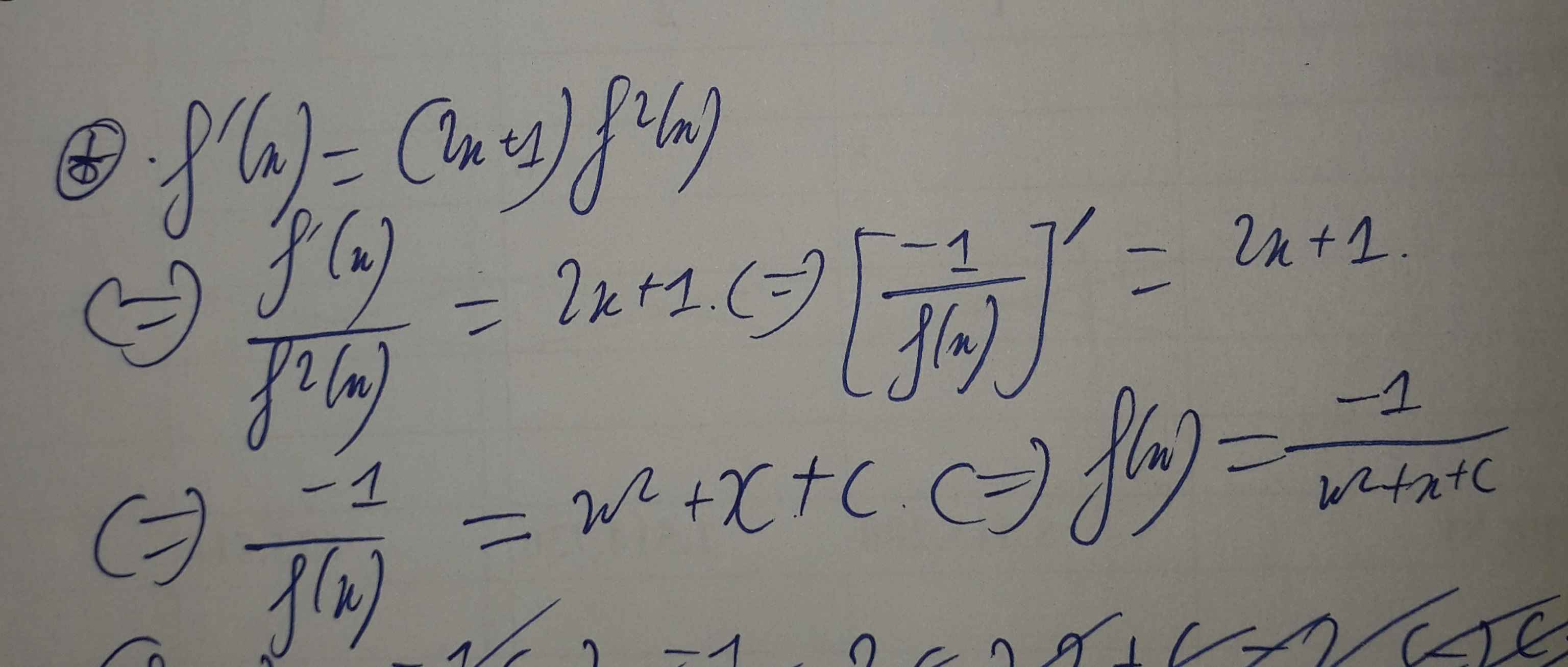
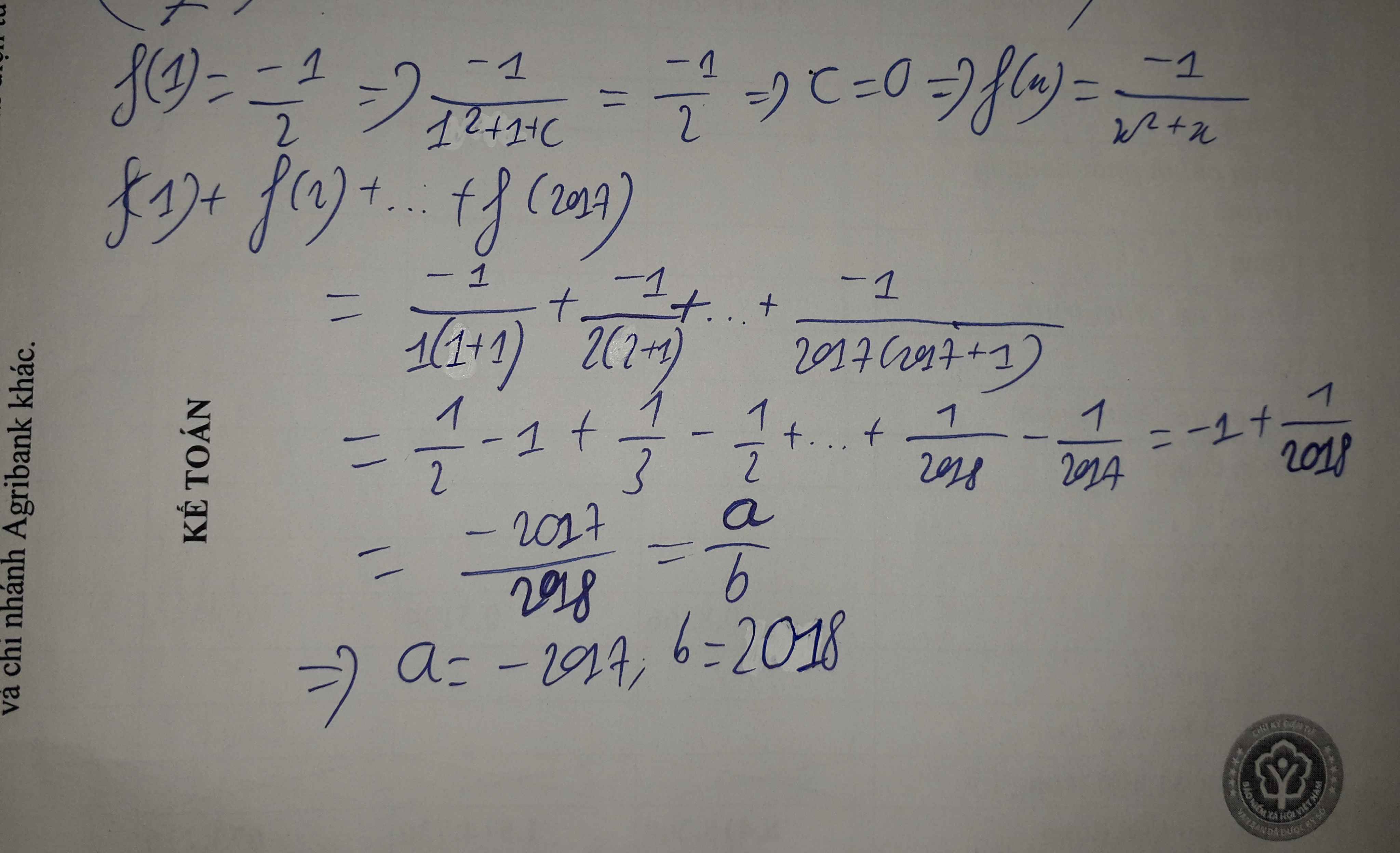
1/Vì x-1 thuộc BC(4,5,6) nên x-1 thuộc {120;240;360;480;,,,}
Suy ra x={119;239;359;479;,,,}
Mà x<400 suy ra x thuộc {119;239;359}
Vì x chia hết 7 suy ra x=119
2/Gọi số học sinh đó = x (x thuộc N*;x<400)
vì x chia 4;5;6 đều dư 1 suy ra x-1 chia hết 4;5;6 nên x-1 thuộc BC(4;5;6)
suy ra x-1 thuộc { 120;240;360;480;,,,}
suy ra x thuộc { 119;239;359;479;,,,}
Vì x<400 suy ra x thuộc {119;239;359;479}
mà x chia hết cho 7 suy ra x=119
Vậy số học sinh của trường đó = 119
1.
BCNN ( 4,5,6 ) = 60
\(\Rightarrow\)x - 1 \(\in\)B ( 60 ) = { 0 ; 60 ; 120 ; 180 ; 240 ; 300 ; 360 ; 420 ; ... }
\(\Rightarrow\)x = { 1 ; 61 ; 121 ; 181 ; 241 ; 301 ; 361 ; 421 }
Mà x < 400 và x \(⋮\)7
Ta thấy x = 301 thỏa mãn các điều kiện trên.
2.
gọi số học sinh của trường đó là a ( a \(\in\)N* )
Theo bài ra : a \(\le\)400 ; a chia 4,5,6 dư 1 ; a \(⋮\)7
a chia 4,5,6 dư 1
\(\Rightarrow\)a - 1 \(⋮\)4,5,6
a - 1 \(\in\)BC ( 4,5,6 )
BCNN ( 4,5,6 ) = 60
\(\Rightarrow\)a - 1 \(\in\)B ( 60 ) = { 0 ; 60 ; 120 ; 180 ; 240 ; 300 ; 360 ; 420 ; ... }
\(\Rightarrow\)a \(\in\){ 1 ; 61 ; 121 ; 181 ; 241 ; 301 ; 361 ; 421 ; ... }
Mà a \(⋮\)7 nên a = 301 thì thỏa mãn các điều kiện trên
Vậy số học sinh trường đó là 301 học sinh