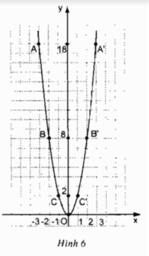
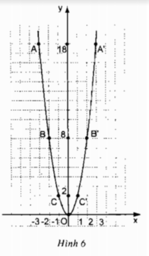
Nhận xét một vài đặc điểm của đồ thị và rút ra những kết luận, tương tự như đã làm đối với hàm y =...
Đọc tiếp
Nhận xét một vài đặc điểm của đồ thị và rút ra những kết luận, tương tự như đã làm đối với hàm y = 2x2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 8 2017
- Đồ thị nằm ở phía dưới trục hoành
- Các cặp điểm M và M’; N và N’; P và P’ đối xứng nhau qua trục Oy
- Điểm O (0;0) là điểm cao nhất của đồ thị.
CM
2 tháng 9 2018
- Đồ thị nằm ở phía dưới trục hoành
- Các cặp điểm M và M’; N và N’; P và P’ đối xứng nhau qua trục Oy
- Điểm O (0;0) là điểm cao nhất của đồ thị.
CM
25 tháng 6 2017
Đồ thị nằm ở phía trên trục hoành
- Các cặp điểm A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy
- Điểm O (0;0) là điểm thấp nhất của đồ thị.
CM
26 tháng 7 2017
Đồ thị nằm ở phía trên trục hoành
- Các cặp điểm A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy
- Điểm O (0;0) là điểm thấp nhất của đồ thị.
CM
23 tháng 9 2019
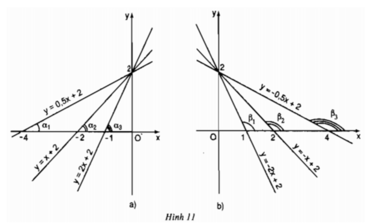
a) Ta có: α 1 < α 2 < α 3 và các giá trị tương ứng của hệ số a trong các hàm số :
0,5 < 1 < 2
Nhận xét: Khi hệ số a dương (a > 0) thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 90o
b) Ta có: β 1 < β 2 < β 3 và các giá trị tương ứng của hệ số a trong các hàm số
-2 < -1 < -0,5
Nhận xét : Khi hệ số a âm (a < 0) thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 180o
CM
2 tháng 7 2017
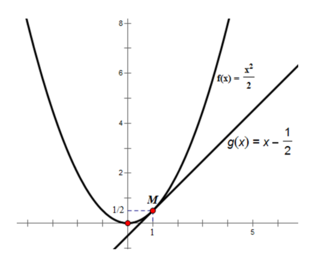
- Giả sử Δx là số gia của đối số tại xo = 1. Ta có:
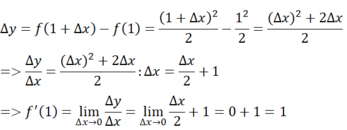
- Đường thẳng có hệ số góc bằng f'(1) = 1 có dạng:
y = 1.x + a hay y = x + a
Mà đường thẳng đó đi qua điểm M(1;1/2) nên có: 1/2 = 1 + a ⇒ a = 1/2 - 1 = -1/2
⇒ đường thẳng đi qua M và có hệ số góc bằng 1 là: y = x – 1/2
Ta có đồ thị như trên. Đường thẳng y = x – 1/2 tiếp xúc với đồ thị hàm số f(x) tại M
CM
14 tháng 7 2019
* Hàm số y = 2x2
- Khi x tăng nhưng luôn luôn âm thì giá trị tương ứng của y giảm
- Khi x tăng nhưng luôn luôn dương thì giá trị tương ứng của y tăng
* Hàm số y = -2x2
- Khi x tăng nhưng luôn luôn âm thì giá trị tương ứng của y tăng
- Khi x tăng nhưng luôn luôn dương thì giá trị tương ứng của y giảm
CM
5 tháng 3 2018
* Hàm số y = 2x2
- Khi x tăng nhưng luôn luôn âm thì giá trị tương ứng của y giảm
- Khi x tăng nhưng luôn luôn dương thì giá trị tương ứng của y tăng
* Hàm số y = -2x2
- Khi x tăng nhưng luôn luôn âm thì giá trị tương ứng của y tăng
- Khi x tăng nhưng luôn luôn dương thì giá trị tương ứng của y giảm
CM
11 tháng 5 2018
Đồ thị hàm số y = ax2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.