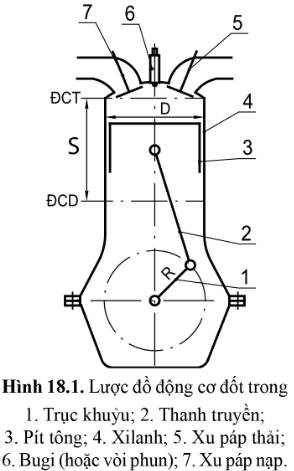
Tìm mối liên hệ giữa hành trình pít tông S và bán kính quay R của trục khuỷu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, Tại \(\alpha = \frac{\pi }{2}\) thì H trùng I, M trùng O nên MH = OI do đó OM = IH.
Xét tam giác AHI vuông tại H có: \(IH = cos\alpha .IA = 8cos\alpha .\)
\( \Rightarrow {x_M} = OM = IH = 8cos\alpha \)
b, Sau khi chuyển động được 1 phút, trục khuỷu quay được một góc là \(\alpha \)
Khi đó \({x_M} = - 3cm \Rightarrow cos\alpha = - \frac{3}{8}\)
Sau khi chuyển động 2 phút, trục khuỷu quay được một góc \(2\alpha \), nên:
\({x_M} = 8cos2\alpha = 8\left( {2{{\cos }^2}\alpha - 1} \right)\)\( = 8\left( {2{{\left( { - \frac{3}{8}} \right)}^2} - 1} \right) \approx - 5,8 cm\)

- Pít tông (4) đang dịch chuyển lên trên. Khi pit tông dịch chuyển lên vị trí cao nhất sẽ đổi chiều chuyển động, và sau đó khi pit tông dịch chuyển xuống vị trí thấp nhất sẽ lại đổi chiều chuyển động.
- Mô tả sự thay đổi thể tích giới hạn bởi đỉnh pít tông và không gian phía trên của xi lanh:
+ Thể tích lớn nhất khi trục khuỷu quay ở vị trí số 6 của kim đồng hồ.
+ Thể tích nhỏ nhất khi trục khuỷu quay ở vị trí số 12 của kim đồng hồ.

- Hình a có đỉnh pit tông ở xa tâm trục khuỷu nhất.
- Hình b, c có đỉnh pit tông gần tâm trục khuỷu nhất.

Trục khuỷu quay theo chiều mũi tên, pít tông sẽ chuyển động lên trên; thể tích giảm dần, nhiệt độ và áp suất phía trên đỉnh pít tông tăng dần.
S=2R