Cho tứ giác ABCD có AB+BD≤AC+CD.chứng minh ab<ac
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)
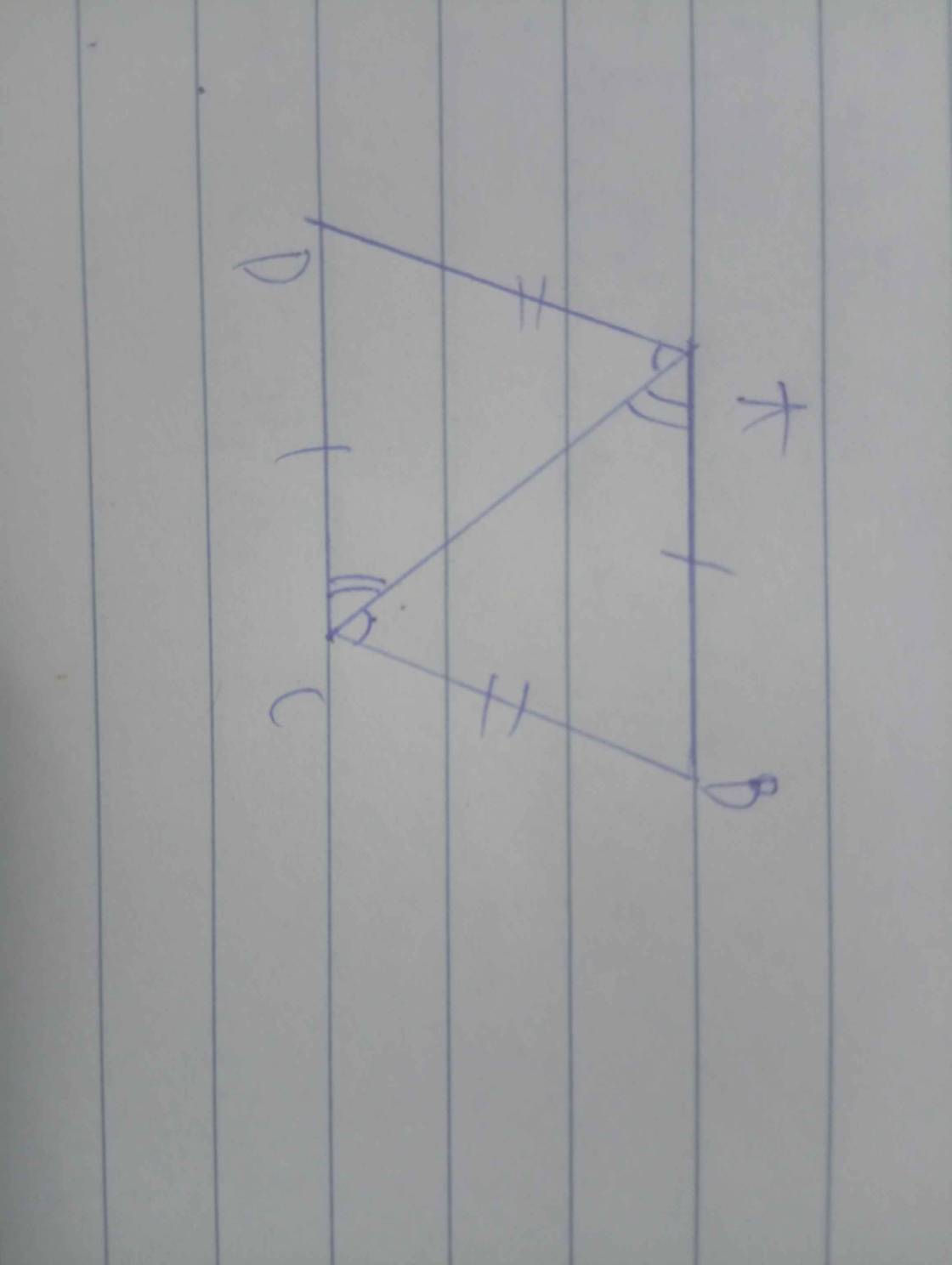

a﴿ Kẻ BN vuông AD, BM vuông CD
Xét tam giác vuông BNA và BMD có
: AB = BC ; góc BNA = 180 độ
‐ góc BAD = 70 độ
nên góc BAN = góc BCD = 70 độ
=> tam giác BMD = tam giác BND ﴾cạnh huyền ‐ góc nhọn﴿
=> BN = BM => BD là phân giác góc D
b﴿ Nối B vs D, do AB = AD nên tam giác ABD cân tại A
khi đó góc ADB = ﴾180 ‐110) :2= 35 độ
=> góc ADC = 70 Do góc ADC + góc BAD = 180 => AB // CD
Và góc BCD = góc ADC = 70 độ
=> ABCD là hình thang cân

Xét tứ giác ABCD có \(\widehat{B}+\widehat{D}=180^0\)
nên ABCD là tứ giác nội tiếp
Xét đường tròn ngoại tiếp tứ giác ABCD có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
\(\widehat{DAC}\) là góc nội tiếp chắn cung DC
mà \(sđ\stackrel\frown{BC}=sđ\stackrel\frown{CD}\)
nên \(\widehat{BAC}=\widehat{DAC}\)
hay AC là tia phân giác của góc A

a) Ta có góc B = 105 độ và góc D = 75 độ.
Vì AB = BC = CD, suy ra tam giác ABC và tam giác BCD là tam giác cân.
Do đó, ta có góc ABC = góc BAC và góc BCD = góc BDC.
Vì góc BAC + góc ABC + góc BCA = 180 độ (tổng các góc trong tam giác ABC bằng 180 độ),
thay giá trị vào ta có góc BAC + góc BAC + góc BCA = 180 độ.
Suy ra góc BAC + góc BCA = 180 độ - góc BAC = góc ABC.
Tương tự, ta có góc BCD + góc BDC = 180 độ - góc BDC = góc BCD.
Vậy ta có góc BAC = góc ABC = góc BCA và góc BCD = góc BDC = góc BCD.
Do đó, AC là tia phân giác của góc A.
b) Ta đã chứng minh được AC là tia phân giác của góc A.
Vì AB = BC = CD, suy ra tam giác ABC và tam giác BCD là tam giác cân.
Vì góc BAC = góc ABC và góc BCD = góc BDC,
nên ta có góc BAC = góc ABC = góc BCA và góc BCD = góc BDC = góc BCD.
Vậy ta có AB || CD.
Do đó, ABCD là hình thang cân.
Giải:
Gọi \(O\) là giao điểm của hai đường chéo \(A C\) và \(B D\).
Xét tam giác \(A B O\), ta có:
\(O A + O B > A B\) (bất đẳng thức tam giác)
Xét tam giác \(D C O\), ta có:
\(O C + O D > C D\) (bất đẳng thức tam giác)
Cộng hai bất đẳng thức trên:
\(A C + B D > A B + C D\)
Mà theo giả thiết:
\(A B + B D \leq A C + C D\)
Cộng hai vế bất đẳng thức ta được:
\(2 A C + B D + C D > 2 A B + B D + C D\)
Rút gọn vế trái và vế phải:
\(2 A C > 2 A B\)
Suy ra: \(A C > A B\), hay \(A B < A C\) \(\left(đpcm\right)\).