Hai (O) và (O') cắt nhau ở A và B (O và O' thuộc 2 nửa mp bờ AB). Kẻ các đường kính BOC và BO'D
a, C/m: 3 điểm C,A,D thẳng hàng
b, Biết OO'= 5cm, OB= 4cm, O'B= 3cm. Tính diện tích tam giác ABC
Em cần gấpp lắm huhu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài (R > r). Hai tiếp tuyến chung AB và A'B' của hai đường tròn (o),(O') cắt nhau tại P(A và A' thuộc đường tròn (O'), B và B' thuộc đường tròn (O)). Biết PA = AB = 4 cm. Tính diện tích hình tròn (O').
Hướng dẫn làm bài:
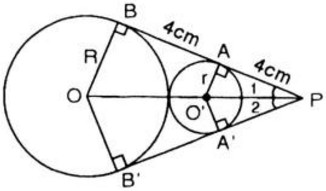
Vì AB là tiếp tuyến chung của (O) và (O’) nên OB ⊥ AB và O’A ⊥ AB
Xét hai tam giác vuông OPB và O’AP, ta có:
ˆA=ˆB=900A^=B^=900
ˆP1P1^ chung
Vậy ΔOBP ~ ∆ O’AP
⇒rR=PO′PO=PAPB=48=12⇒R=2r⇒rR=PO′PO=PAPB=48=12⇒R=2r
Ta có PO’ = OO’ = R + r = 3r (do AO’ là đường trung bình của ∆OBP)
Áp dụng định lí Py-ta-go trong tam giác vuông O’AP
O’P = O’A2 + AP2 hay (3r)2 = r2 + 42 ⇔ 9r2 = r2 + 16 ⇔ 8 r2 =16 ⇔ r2 = 2
Diện tích đường tròn (O’;r) là: S = π. r2 = π.2 = 2π (cm2)

Vì AB là tiếp tuyến chung của (O) và (O’) nên OB ⊥ AB và O’A ⊥ AB
Xét hai tam giác vuông OPB và O’AP, ta có:
ˆA=ˆB=900A^=B^=900
ˆP1P1^ chung
Vậy ΔOBP ~ ∆ O’AP
⇒rR=PO′PO=PAPB=48=12⇒R=2r⇒rR=PO′PO=PAPB=48=12⇒R=2r
Ta có PO’ = OO’ = R + r = 3r (do AO’ là đường trung bình của ∆OBP)
Áp dụng định lí Py-ta-go trong tam giác vuông O’AP
O’P = O’A2 + AP2 hay (3r)2 = r2 + 42 ⇔ 9r2 = r2 + 16 ⇔ 8 r2 =16 ⇔ r2 = 2
Diện tích đường tròn (O’;r) là: S = π. r2 = π.2 = 2π (cm2)


(O; R) và (O’; R’) tiếp xúc ngoài với nhau
⇒ OO’ = R + r.
O’A ⊥ BP, OB ⊥ BP ⇒ O’A // OB
⇒ ΔPAO’  ΔPBO
ΔPBO

⇒ OB = 2.O'A hay R = 2.r
và OP = 2.O’P ⇒ O’P = OO’ = R + r = 3.r
ΔO’AP vuông tại A nên:
O ’ P 2 = O ’ A 2 + A P 2
⇔ ( 3 r ) 2 = r 2 + 4 2 ⇔ 8 r 2 = 16 ⇔ r 2 = 2
Diện tích hình tròn (O’; r) là: S = π . r 2 = 2 π ( c m 2 ) .


(O; R) và (O’; R’) tiếp xúc ngoài với nhau
⇒ OO’ = R + r.
O’A ⊥ BP, OB ⊥ BP ⇒ O’A // OB
⇒ ΔPAO’  ΔPBO
ΔPBO

⇒ OB = 2.O'A hay R = 2.r
và OP = 2.O’P ⇒ O’P = OO’ = R + r = 3.r
ΔO’AP vuông tại A nên: O ' P 2 = O ' A 2 + A P 2
⇔ ( 3 r ) 2 = r 2 + 4 2 ⇔ 8 r 2 = 16 ⇔ r 2 = 2
Diện tích hình tròn (O’; r) là: S = π · r 2 = 2 π cm 2

Gọi giao điểm của MB với (O;r) là H, giao điểm của MD với (O;r) là K
Theo đề, ta có: OH\(\perp\)MB tại H và OK\(\perp\)MD tại K
Xét (O) có
OH,OK là khoảng cách từ tâm O đến cách dây AB,CD
AB,CD là các dây
OH=OK(=r)
Do đó: AB=CD
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>HA=HB=AB/2
Ta có: ΔOCD cân tại O
mà OK là đường cao
nên K là trung điểm của CD
=>\(CK=KD=\dfrac{CD}{2}\)
mà CD=AB và \(HA=HB=\dfrac{AB}{2}\)
nên CK=KD=HA=HB
Xét ΔOHM vuông tại H và ΔOKM vuông tại K có
OH=OK
OM chung
Do đó: ΔOHM=ΔOKM
=>MH=MK
Ta có: MA+AH=MH
MC+CK=MK
mà AH=CK và MH=MK
nên MA=MC
Xét ΔMBD có \(\dfrac{MA}{AB}=\dfrac{MC}{CD}\)
nên AC//BD
=>\(sđ\stackrel\frown{AB}=sđ\stackrel\frown{CD}\)

Khi vẻ hình ta sẽ biết đuợc đây là hai tia đối nhau , nên Ô nằm giữa A và B

vì C, B cùng thuộc đường tròn (O) => OB=OC => tam giác OBC cân tại O => góc OCB= góc OBC (1)
tương tự góc O'BD= góc O'DB (2)
vì BD là tia pg của góc OBO' => góc OBC= góc DBO' (3)
từ (1) , (2) , (3)=> góc OBC=OCB=O'DB=O'BD
=> góc BOC = góc DO'B
a: góc CAB=1/2*sđ cung CB=90 độ
góc BAD=1/2*sđ cung BD=90 độ
góc CAD=góc CAB+góc BAD
=90 độ+90 độ=180 độ
=>C,A,D thẳng hàng